questão sobre ponto
2 participantes
Página 1 de 1
questão sobre ponto
por rebecaszz Qui 02 Mar 2023, 08:36
A linha poligonal da figura parte da origem e passa por todos os pontos do plano que têm coordenadas inteiras não negativas, de acordo com o padrão indicado. A unidade de comprimento nos eixos é 1 cm. O comprimento da poligonal da origem até um ponto (a, b) é chamado de lonjura de (a, b); por exemplo, a lonjura de (1,2) é 5 cm.
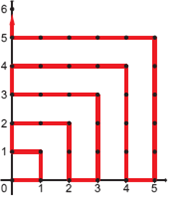
a) Determine a lonjura dos pontos (3,2) e (0,4).
b) Quantos pontos de coordenadas inteiras estão contidos no interior e nos lados do quadrado cujos vértices são (0,0), (n,0), (n, n) e (0,n)?
c) Explique por que a lonjura do ponto (n,n) é [latex]n^{2}+n[/latex]
d) Qual é o ponto cuja lonjura é 425?
a) Determine a lonjura dos pontos (3,2) e (0,4).
b) Quantos pontos de coordenadas inteiras estão contidos no interior e nos lados do quadrado cujos vértices são (0,0), (n,0), (n, n) e (0,n)?
c) Explique por que a lonjura do ponto (n,n) é [latex]n^{2}+n[/latex]
d) Qual é o ponto cuja lonjura é 425?
Última edição por rebecaszz em Dom 05 Mar 2023, 18:40, editado 1 vez(es)
rebecaszz- Recebeu o sabre de luz
- Mensagens : 101
Data de inscrição : 21/02/2023
Idade : 19
Localização : campinas, sp
Re: questão sobre ponto
por DaoSeek Sex 03 Mar 2023, 18:35
Na letra (a) basta contar. O item (b) parece não relacionado a questão, mas justamente por isso é uma dica para o item(c). No caso observamos que um quadrado n x n terá n+1 pontos de base e n+1 de altura, totalizando (n+1)² = n²+2n+1.
No item (c) notamos que o caminho partindo de (0,0) até (n,n) passa por todos os pontos do quadrilátero exceto por um lado. Ou seja, o comprimento da linha poligonal será justamente a quantidade de pontos no interior do quadrado subtraido pelos pontos que se encontram no lado do quadrado, isto é, n+1. Portanto a resposta é
(n+1)² - (n+1) = n² + n
Por fim, no item (d) notamos que se n = 20, então n² +n = 420. Daí a lonjura de (20,20) é 420. Portanto, o ponto cuja lonjura é 425 encontra-se 5 unidades abaixo de (20,20). Ou seja, é o ponto (20, 15)
No item (c) notamos que o caminho partindo de (0,0) até (n,n) passa por todos os pontos do quadrilátero exceto por um lado. Ou seja, o comprimento da linha poligonal será justamente a quantidade de pontos no interior do quadrado subtraido pelos pontos que se encontram no lado do quadrado, isto é, n+1. Portanto a resposta é
(n+1)² - (n+1) = n² + n
Por fim, no item (d) notamos que se n = 20, então n² +n = 420. Daí a lonjura de (20,20) é 420. Portanto, o ponto cuja lonjura é 425 encontra-se 5 unidades abaixo de (20,20). Ou seja, é o ponto (20, 15)
DaoSeek- Jedi
- Mensagens : 316
Data de inscrição : 29/07/2022
Tópicos semelhantes» Ponto C sobre reta.
» Questão sobre ponto médio de triângulo!!!
» Questão sobre reta tangente em um ponto da parábola.
» Dúvida em questão sobre distancia entre ponto
» Ponto sobre o eixo
» Questão sobre ponto médio de triângulo!!!
» Questão sobre reta tangente em um ponto da parábola.
» Dúvida em questão sobre distancia entre ponto
» Ponto sobre o eixo
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
