(IME 2017) análise combinatória

por mhope Qui 15 Dez 2022, 17:40

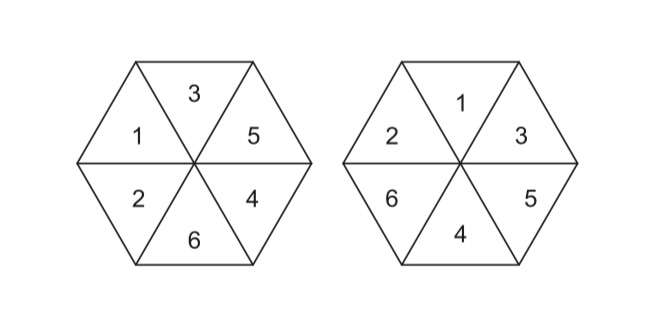
Um hexágono é dividido em 6 triângulos equiláteros. De quantas formas podemos colocar os números de 1 a 6 em cada triângulo, sem repetição, de maneira que a soma dos números em três triângulos adjacentes seja sempre múltiplo de 3? Soluções obtidas por rotação ou reflexão são diferentes, portanto as figuras abaixo mostram duas soluções distintas.

(IME 2017) análise combinatória Cb22a810

Amigos, queria saber se minha resolução está certa, aqui está:

Achei os trios cuja soma é um número múltiplo de 3.

(1,2,3) (1,2,6) (1,3,5) (1,5,6) (1,6,2) (4,5,6) (6,4,2) e (5,4,3)

Só que os valores podem mudar de posição, então 3! para os 8

Assim, 8.3! = 48

por **Elcioschin** Qui 15 Dez 2022, 19:20

Vc repetiu 126 e 162

Possibildadesde somas

Soma 6 ---> 1 + 2 + 3 ou 1 + 3 + 2 ou 2 + 1 + 3 ou 2 + 3 + 1 ou 3 + 1 + 2 ou 3 + 2 + 1
Soma 9 ---> 1 + 2 + 6 ---> idem
Soma 9 ---> 1 + 3 + 5 ---> idem
Soma 12 --> 1 + 5 + 6 ---> idem
Soma 12 --> 2 + 4 + 6 ---> idem
Soma 12 --> 3 + 4 + 5 ---> idem
Soma 15 --> 4 + 5 + 6 ---> idem

(IME 2017) análise combinatória

(IME 2017) análise combinatória

Re: (IME 2017) análise combinatória

Um fórum livre e democrático.