Sistemas Lineares
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Sistemas Lineares
por andreas ratiner Sáb 15 Out 2022, 22:06
Considere k ∈ IR O sistema de equações lineares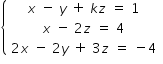 
não possui solução quando
A
B
C
D
E
k = 0
Última edição por andreas ratiner em Dom 16 Out 2022, 00:45, editado 1 vez(es)
andreas ratiner- Recebeu o sabre de luz
- Mensagens : 103
Data de inscrição : 14/10/2021
Re: Sistemas Lineares
por Fibonacci13 Sáb 15 Out 2022, 23:18
Olá, Andreas.
x - y +kz = 1 (I)
x - 2z = 4 (II)
2x - 2y+3z = -4 (III)
Se, k = 3/2:
x - y + 3z/2 = 1 (I)
x - 2z = 4 (II)
2x - 2y + 3z = -4 (III)
Multiplicando toda a equação (I) por 2, temos:
2x - 2y + 3z = 2 (I)
x - 2z = 4 (II)
2x - 2y + 3z = -4 (III)
Veja que as equações I e III possuem os mesmos membros esquerdos, mas possuem os membros direitos diferentes. Quando temos isso, possuímos um sistema sem solução.
x - y +kz = 1 (I)
x - 2z = 4 (II)
2x - 2y+3z = -4 (III)
Se, k = 3/2:
x - y + 3z/2 = 1 (I)
x - 2z = 4 (II)
2x - 2y + 3z = -4 (III)
Multiplicando toda a equação (I) por 2, temos:
2x - 2y + 3z = 2 (I)
x - 2z = 4 (II)
2x - 2y + 3z = -4 (III)
Veja que as equações I e III possuem os mesmos membros esquerdos, mas possuem os membros direitos diferentes. Quando temos isso, possuímos um sistema sem solução.
Fibonacci13- Mestre Jedi
- Mensagens : 872
Data de inscrição : 14/09/2019
Idade : 22
Localização : São Paulo
andreas ratiner- Recebeu o sabre de luz
- Mensagens : 103
Data de inscrição : 14/10/2021
Tópicos semelhantesPiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
