Problema de menor distância entre dois pontos.

por Valéria Oliveira Ter 04 Out 2022, 15:03

Olá.

São dados dois pontos A e B situados ambos em um dos semiplanos determinados pela reta CD, conforme a figura a seguir.
Problema de menor distância entre dois pontos. EzOhqAS9wltdsAAAAALm0sGwAAAIAxKK8AAAAwBuUVAAAAxqC8AgAAwBiUVwAAABiD8goAAABjUF4BAABgDMorAAAAjEF5BQAAgDEorwAAADAG5RUAAADGoLwCAADAGP8Pn+VrFsngTbkAAAAASUVORK5CYII=

Problema de menor distância entre dois pontos. EzOhqAS9wltdsAAAAALm0sGwAAAIAxKK8AAAAwBuUVAAAAxqC8AgAAwBiUVwAAABiD8goAAABjUF4BAABgDMorAAAAjEF5BQAAgDEorwAAADAG5RUAAADGoLwCAADAGP8Pn+VrFsngTbkAAAAASUVORK5CYII=

A menor distância, em metros, entre A e B, quando se toca a reta CD, é igual a
A) 38
B) 39
C) 40
D) 41
E) 42
Gabarito: D

Minha interpretação da questão está errada, agradeço qualquer ajuda.

por **Elcioschin** Ter 04 Out 2022, 16:53

Poste o ponto B', simétrico de B em relação à reta CD ---> H₂B' = 22

Trace a reta AB' e seja P o ponto de contato dela com o segmento H₁H₂

Triângulos AH₁P e B'H₂P são semelhantes: calcule AP e BP

Caso prático na Física - Óptica

CD é um espelho plano A é o olho de um observador, B é um objeto, B' é a imagem de B e BP + PA é o trajeto do raio luminoso de B até A
Note que a luz é inteligente, eficaz e econômica: ela percorre o menor caminho, no menor tempo

por Valéria Oliveira Ter 04 Out 2022, 17:28

Aí está uma sacada que eu ainda não tenho com a mesma astúcia da luz. Só a experiência mesmo para me iluminar a inteligência. Obrigada, @Elcioschin, gostei do exemplo!

por **Elcioschin** Ter 04 Out 2022, 18:08

Existem outras soluções mas envolvem derivadas e dá mais trabalho.

Eis o passo-a-passo da solução da luz:

Seja AP = x ---> BP = 9 - x

AH₁/PH₁ = B'H₂/PH₂ ---> 18/x = 22/(9 - x) ---> AP = x = 4,05 --> BP = 4,95

(AP)² = (AH₁)² + (PH₁₎)² ---> (AP)² = 18² + 4,05² ---> AP = 18,45

(BP)² = (B'H₂)² + (PH₂₎)² ---> (BP)² = 22² + 4,55² ---> AP = 22,55

d = AP + BP ---> d = 18,45 + 22,55 ---> d = 41 m

Uma curiosidade: Seja PÂH₁ = θ e P^BH₂ = φ

tgθ = 4,05/18 ---> tgθ = 0,225
tgφ = 4,95/22 --> tgφ = 0,225 ---> Conclusão ---> φ = θ ---> A^PB = 2.θ

por Valéria Oliveira Ter 04 Out 2022, 20:04

Uma questão, várias perspectivas
Deixo uma ilustração:

Problema de menor distância entre dois pontos. Whatsa13

por **Elcioschin** Qua 05 Out 2022, 11:13

Complementando o desenho da Valéria, incluindo a imagem A' de A no espelho e mais algumas informações:

Problema de menor distância entre dois pontos. Camin10

por **Medeiros** Qui 06 Out 2022, 03:44

O exercício não pediu mas pelo que entendi da discussão a Valéria quer calcular o ponto exato onde se deve tocar a reta CD para obter a menor distância AB. Se assim for, apresento uma sugestão simples.

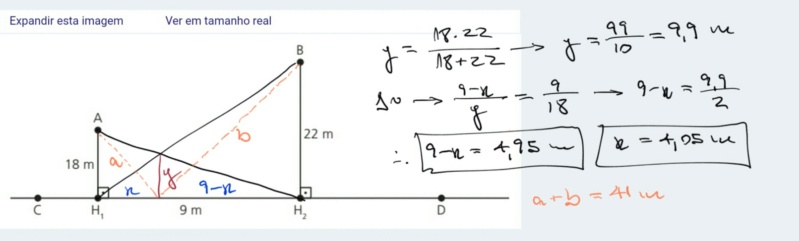
Problema de menor distância entre dois pontos. Scre1870

no desenho, y é metade da média harmônica entre os postes A e B. Após considerei a semelhança de triângulos do poste A (usei este porque a medida 18 deixa a conta mais fácil).