Progressões Geométricas

por Belkin Dom 07 Ago 2022, 00:23

Acima de uma reta r foi desenhado um quadrado de lado 4 cm. Outros quadrados foram desenhados, de modo que o lado de cada quadrado, a partir do segundo, é metade do lado do quadrado anterior, conforme o desenho.

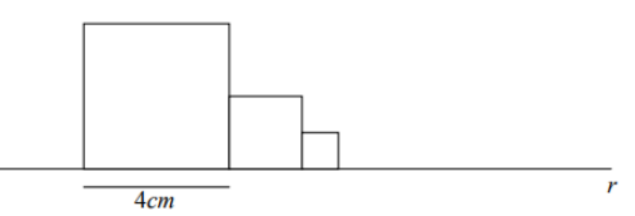
Progressões Geométricas 1418_2_325454_3447048_

Desenhando-se mais quadrados, seguindo a regra acima indefinidamente, podemos concluir que

A

a soma das áreas dos quadrados não chegará a 22 cm².
B

a soma das áreas dos quadrados não chegará a 20 cm².
C

a soma das áreas dos quadrados aumenta, tendendo ao infinito.
D

a soma das áreas dos quadrados aumenta, tendendo a 32 cm².
E

a soma das áreas dos quadrados aumenta, tendendo a 42 cm².

por Matheus Fillipe Dom 07 Ago 2022, 03:13

A área do quadrado é dada pelo lado elevado ao quadrado. Se cada quadrado tem a métade do lado que o anterior, a área total será:

[latex]A = 4^2 + 2^2 + 1^2 + (\frac{1}{2})^2 + (\frac{1}{4})^2 ...[/latex]

Que também pode ser escrita como um somatório:

[latex] A=\sum_{n=0}^\infty (\frac{4}{2^n})^2 = \sum_{n=0}^\infty \frac{16}{(2^n)^2} = 16 \times \sum_{n=0}^\infty \frac{1}{(2^n)^2} = \times \sum_{n=0}^\infty \frac{1}{4^n} = \times \sum_{n=0}^\infty (\frac{1}{4})^n [/latex]

Que é a soma de uma PG infinita. Sabendo que:

[latex]\sum_{n=0}^\infty (\frac{1}{r})^n = \frac{1}{1-r}[/latex]

Temos:

[latex]A = 16 \times \frac{1}{1-\frac{1}{4}} = \frac{4 \times 16}{3} = \frac{64}{3} = 21.3333...[/latex]

Então A).