Função trigonométrica - Enem Digital 2020
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Função trigonométrica - Enem Digital 2020
Função trigonométrica - Enem Digital 2020
ENEM 2020 DIGITAL
A
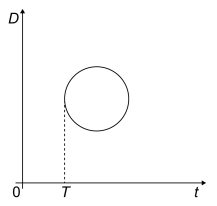
B
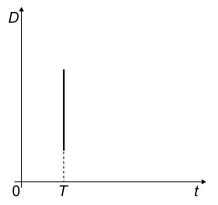
C

D
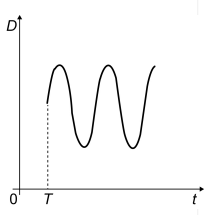
E
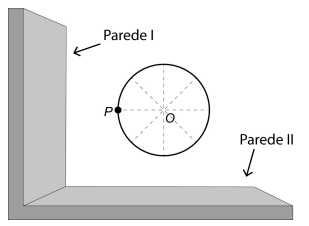
A figura ilustra a vista superior de um brinquedo gira-gira em um parque de diversões, no qual a linha contínua, em formato circular tendo O como seu centro, indica o assento onde as crianças se posicionam no brinquedo. O ponto P indica a posição ocupada por uma criança, em um instante de tempo T, quando o brinquedo está girando continuamente no sentido anti-horário (com O fixo), e velocidade constante por várias voltas.

O brinquedo está situado nas proximidades de duas paredes verticais e perpendiculares entre si. Seja D a distância de P até a parede I.
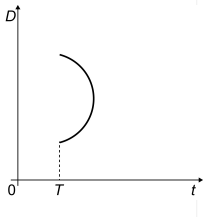
O gráfico que melhor representa, em função do tempo t a partir do instante T, a distância D é
A

B

C

D

E

- Gabarito:
- Alternativa "C"
Olá, boa noite, tenho algumas dúvidas em relação a essa questão
I - o fato do movimento ser anti-horário traz qual consequência?
II - Quais características diferenciam esse gráfico (senoidal) em relação a um cossenoide? Achei que era pelo decréscimo ou crescimento nos quadrantes, mas vi em uma vídeo aula de resolução dessa questão que é devido a posição inicial ser zero , porém não entendi/visualizei isso no gráfico
Desde já, muito obrigada!!
 Re: Função trigonométrica - Enem Digital 2020
Re: Função trigonométrica - Enem Digital 2020
EU entendo assim. O sentido não altera a resolução pois tanto no horário como no anti horário as distâncias serão simétricas, dA= DB)
A questão nao precisa saber o tipo de função, senoidal ou cosssenoidal. Sabemos que é uma função periódica (que se repete)e que inicia no menor ponto possível, portanto basta analisar a distância no gráfico.
Veja que no gráfico C ele começa na menor distância (é o que ocorre na realidade) e no gráfico D, veja que acontecerá distâncias menores que a inicial o que não pode ocorrer.
Portanto o gráfico tem semelhança com a função seno, que inicia no menor ponto, depois é crescente até seu ápice e depois decresce ao seu menor ponto.
No gráfico do cosseno ocorre o inverso. Sairia do maior ponto para o menor e depois retornaria ao maior
A questão nao precisa saber o tipo de função, senoidal ou cosssenoidal. Sabemos que é uma função periódica (que se repete)e que inicia no menor ponto possível, portanto basta analisar a distância no gráfico.
Veja que no gráfico C ele começa na menor distância (é o que ocorre na realidade) e no gráfico D, veja que acontecerá distâncias menores que a inicial o que não pode ocorrer.
Portanto o gráfico tem semelhança com a função seno, que inicia no menor ponto, depois é crescente até seu ápice e depois decresce ao seu menor ponto.
No gráfico do cosseno ocorre o inverso. Sairia do maior ponto para o menor e depois retornaria ao maior
____________________________________________

_______________________________
"Ex nihilo nihil fit"
petras- Monitor

- Mensagens : 2117
Data de inscrição : 10/06/2016
Idade : 59
Localização : bragança, sp, brasil
 Re: Função trigonométrica - Enem Digital 2020
Re: Função trigonométrica - Enem Digital 2020
Muito obrigada pela ajuda
a função cosseno nunca sai do mínimo ?
a função cosseno nunca sai do mínimo ?
 Re: Função trigonométrica - Enem Digital 2020
Re: Função trigonométrica - Enem Digital 2020
____________________________________________

_______________________________
"Ex nihilo nihil fit"
petras- Monitor

- Mensagens : 2117
Data de inscrição : 10/06/2016
Idade : 59
Localização : bragança, sp, brasil
Ana Laura Guimarães gosta desta mensagem
 Re: Função trigonométrica - Enem Digital 2020
Re: Função trigonométrica - Enem Digital 2020
Então, essa é a minha dúvida, qnd não tiver nenhuma informação sobre qual é a lei da função eu posso considerar que é a original e distinguir cosseno e seno pela origem?
Se o enunciado não fornecer a função, por exemplo, essa que você colocou f(x) = 1 - cos(x) , oq eu usaria para saber que é cosseno e não seno?
Se o enunciado não fornecer a função, por exemplo, essa que você colocou f(x) = 1 - cos(x) , oq eu usaria para saber que é cosseno e não seno?
 Re: Função trigonométrica - Enem Digital 2020
Re: Função trigonométrica - Enem Digital 2020
Olá, Ana. Não precisa "usar" nada. A função seno e cosseno tem comportamentos similares e de muitas formas podem ficar iguais. Veja o seguinte gráfico:Ana Laura Guimarães escreveu:Então, essa é a minha dúvida, qnd não tiver nenhuma informação sobre qual é a lei da função eu posso considerar que é a original e distinguir cosseno e seno pela origem?
Se o enunciado não fornecer a função, por exemplo, essa que você colocou f(x) = 1 - cos(x) , oq eu usaria para saber que é cosseno e não seno?

Isso é função seno ou cosseno?
Bem, esse é o gráfico tanto de y = sen(x), como de y = cos(x-pi/2)
Ah então "como saber qual é"? Não existe saber qual é, ambas estão corretas. Por exemplo, em um caso que é uma questão multipla escolhas exatamente de olhar pra esse gráfico e dizer qual sua função... a letra que tivesse uma dessas 2 funções seria a correta. Se houvesse ambas, é caso de anulação.
Procure uma calculadora gráfica e experimente 1 pouco para entender melhor como elas se comportam. Eu usei essa aqui ó: https://pt.symbolab.com/graphing-calculator

GBRezende- Jedi

- Mensagens : 227
Data de inscrição : 18/10/2017
Idade : 27
Localização : Rio de Janeiro, RJ, Brasil
Ana Laura Guimarães gosta desta mensagem
 Re: Função trigonométrica - Enem Digital 2020
Re: Função trigonométrica - Enem Digital 2020
Entendi, muito obrigada pela explicação, dei uma olhada no site que você indicou, bem interessante.GBRezende escreveu:Olá, Ana. Não precisa "usar" nada. A função seno e cosseno tem comportamentos similares e de muitas formas podem ficar iguais. Veja o seguinte gráfico:Ana Laura Guimarães escreveu:Então, essa é a minha dúvida, qnd não tiver nenhuma informação sobre qual é a lei da função eu posso considerar que é a original e distinguir cosseno e seno pela origem?
Se o enunciado não fornecer a função, por exemplo, essa que você colocou f(x) = 1 - cos(x) , oq eu usaria para saber que é cosseno e não seno?
Isso é função seno ou cosseno?
Bem, esse é o gráfico tanto de y = sen(x), como de y = cos(x-pi/2)
Ah então "como saber qual é"? Não existe saber qual é, ambas estão corretas. Por exemplo, em um caso que é uma questão multipla escolhas exatamente de olhar pra esse gráfico e dizer qual sua função... a letra que tivesse uma dessas 2 funções seria a correta. Se houvesse ambas, é caso de anulação.
Procure uma calculadora gráfica e experimente 1 pouco para entender melhor como elas se comportam. Eu usei essa aqui ó: https://pt.symbolab.com/graphing-calculator
 Re: Função trigonométrica - Enem Digital 2020
Re: Função trigonométrica - Enem Digital 2020
As informações do enunciado e as alternativas é que permitirão você definir qual será a função.Ana Laura Guimarães escreveu:Então, essa é a minha dúvida, qnd não tiver nenhuma informação sobre qual é a lei da função eu posso considerar que é a original e distinguir cosseno e seno pela origem?
Se o enunciado não fornecer a função, por exemplo, essa que você colocou f(x) = 1 - cos(x) , oq eu usaria para saber que é cosseno e não seno?
____________________________________________

_______________________________
"Ex nihilo nihil fit"
petras- Monitor

- Mensagens : 2117
Data de inscrição : 10/06/2016
Idade : 59
Localização : bragança, sp, brasil
Ana Laura Guimarães gosta desta mensagem
 Re: Função trigonométrica - Enem Digital 2020
Re: Função trigonométrica - Enem Digital 2020
Entendi, muito obrigada petras ;]petras escreveu:As informações do enunciado e as alternativas é que permitirão você definir qual será a função.Ana Laura Guimarães escreveu:Então, essa é a minha dúvida, qnd não tiver nenhuma informação sobre qual é a lei da função eu posso considerar que é a original e distinguir cosseno e seno pela origem?
Se o enunciado não fornecer a função, por exemplo, essa que você colocou f(x) = 1 - cos(x) , oq eu usaria para saber que é cosseno e não seno?
 Tópicos semelhantes
Tópicos semelhantes» ENEM 2020 DIGITAL
» ENEM 2020 DIGITAL - Sociologia
» UFRGS 2020 - Q43 - função trigonométrica
» EsFCEx 2020 Função trigonométrica
» (ENEM 2019) Pistão de motor - Função trigonométrica
» ENEM 2020 DIGITAL - Sociologia
» UFRGS 2020 - Q43 - função trigonométrica
» EsFCEx 2020 Função trigonométrica
» (ENEM 2019) Pistão de motor - Função trigonométrica
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos














