Circunferência e reta

Considere uma circunferência de raio 1 e centro no ponto (4,2). Denote por (4,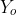) e (4,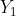), com os dois pontos da circunferência cuja abscissa é 4. Seja r a reta que tem inclinação 3/5 e passa pelo ponto (4,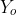). Seja s a reta que intercepta a reta r no ponto de abscissa -1 passa pelo ponto (0,-1). Se a reta s intercepta a circunferência em dois pontos, então é correto afirmar que as coordenadas desses dois pontos são:



Gab: A.

Equação da circunferência:

(y-y0)²+(x-x0)²=R
(y-2)² + (x-4)² = 1

Vamos achar os pontos onde a abscissa é'4:

x = 4

(y-2)² + (4-4)² = 1
(y-2)² = 1
y-2=±1
y' = 3
y" = 1

(4,1) e (4,3)

Reta r:

Passa pelo ponto (4,1) e inclinação 3/5

y-y0 = m (x-x0)
r: y - 1 = (3/5)( x - 4)

Vamos encontrar o ponto onde a abscissa é -1

x = -1

y - 1 = (3/5)(-1-4)
y - 1 = -3
y = -2

(-1,-2)

Reta S passa pelos pontos (-1,-2) e (0,-1)


-2-(-1) = m (-1-0)
m = 1

y - (-1 )= (x - 0)

S: x = y + 1


Vamos substituir a reta S na circunferência, a fim de achar os pontos de interseção:

(y-2)² + (x-4)² = 1
(y-2)² + (y + 1 -4)² = 1
(y-2)² + (y-3)² = 1
y²-4y+4+y²-6y+9=1
2y²-10y+12 = 0
y² - 5y + 6 = 0
(y-3)(y-2) = 0

y' = 3 e y'' = 2

Substituindo y para achar x

x = y+1
x' = 4 e x" = 3

Logo os pontos são:

(4,3) e (3,2)

Uma figura para visualização da solução:

Muito obrigado pelas resoluções!