números complexos

por Ana Clara Macêdo Ter 21 Jun 2022, 16:27

números complexos 0_3fca2034b5666ff4c5db86a02b51cd0b_32.jpg

No sistema de coordenadas cartesianas ortogonais xOy mostrado acima, estão representados, esquematicamente, os pontos 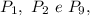$números complexos D0322b762f46572c715464455652d2e5$ correspondentes aos países Costa Rica, Honduras e Panamá, respectivamente, e os pontos 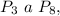$números complexos D4a2ceed8837abe634b3d41f008908dd$ correspondentes às ilhas fictícias onde se desenvolve a trama de Jurassic Park. A tabela mostra as coordenadas desses pontos. No sistema, cada ponto (x, y) está identificado com um número complexo z = x + iy, em que i é a unidade complexa imaginária. Os pontos Pk, com 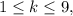$números complexos 89b9ebb8f2084200fa587d9855be3290$ correspondem aos números complexos zk, que representam as ilhas e os países.
A partir dessas informações, julgue o item subsequente:
"O número complexo $números complexos 85de3df2e5b4b3d5e573e1a9087c536c$ é, de fato, um número real".
a)certo
b)errado

Alguém poderia me explicar como se resolve essa questão (de forma detalhada, se possível)? Esse z₂seria as coordenadas do ponto P₂?

por **Elcioschin** Ter 21 Jun 2022, 16:43

z2 = 6 + 6.i ---> z2 = 6.(√2).[√2/2 + i.√2/2] ---> z2 = 6.√2.[cos(pi/4) + i.sen(pi/4)]

(z2)¹²⁰ = (6.√2).[cos(120.pi/4) + i.sen(120.pi/4)] --->

(z2)¹²⁰ = (6.√2).[cos(15.2.pi) + i.sen(15.2.pi)]

cos(15.2pi) = 1 ---> sen(15.2.pi) = 0 ---> Real

por Ana Clara Macêdo Ter 21 Jun 2022, 17:34

Não entendi como "6+6i" vira "6.(√2).[√2/2 + i.√2/2]". Qual o nome desse conteúdo?

por **Elcioschin** Ter 21 Jun 2022, 18:13

O conteúdo é Álgebra - Números complexos:
Experimente desenvolver as contas do 2º membro, para ver:

z2 = 6.(√2).[√2/2 + i.√2/2]

z2 = 6.(√2) é o módulo do numero complexo

por Conteúdo patrocinado

números complexos

números complexos

Re: números complexos

Re: números complexos

Re: números complexos

Re: números complexos

Um fórum livre e democrático.