Semelhança de triângulos

por Bnlla Sáb 07 maio 2022, 16:03

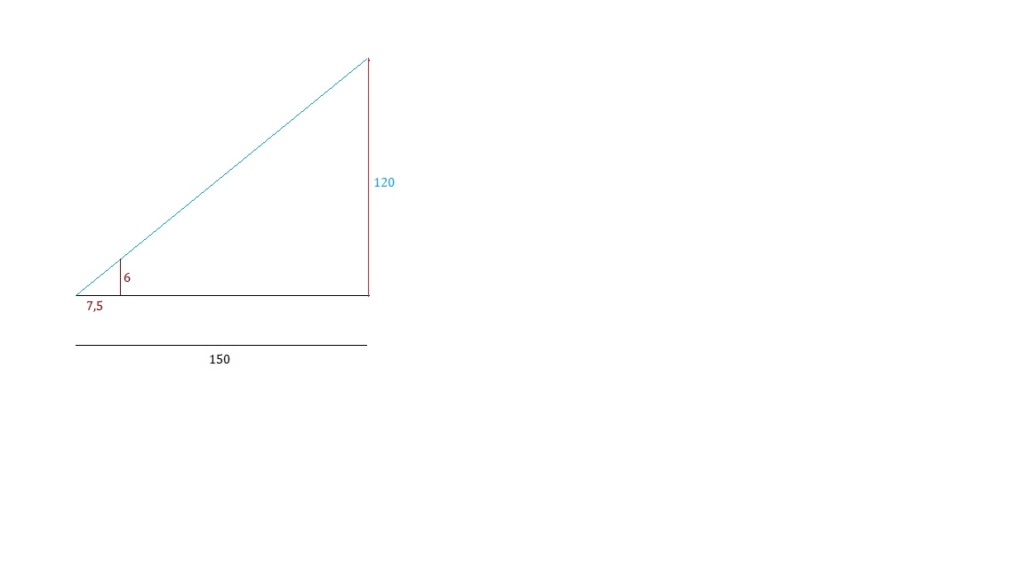
Os engenheiros de uma construtora compraram um terreno na beira de uma praia e estão decidindo a altura do prédio que irão construir, preocupando-se com a sombra que será projetada na praia durante a manhã. Primeiramente, eles verificaram que o sol nasce exatamente atrás de onde será a entrada do prédio e se põe no mar, exatamente à frente de onde será a entrada. Além disso, eles observaram que a distância entre a futura frente do prédio e a praia é de exatamente 150 metros. Analisando um poste de 6 metros de altura na rua em que o prédio será construído, os engenheiros montaram uma tabela que relaciona a variação do comprimento da sombra ao tempo.

Considere que cada andar do prédio terá três metros

de altura e que a distância entre o poste e o terreno é

desprezível.

Os engenheiros concluíram que um prédio de

A) 12 andares gerará sombra na praia até as 10:00.

B) 17 andares gerará sombra na praia até as 07:00.

C) 30 andares gerará sombra na praia até as 12:00.

D) 36 andares gerará sombra na praia até as 06:00.

E) 40 andares gerará sombra na praia até as 08:00.

Resposta: E

Dúvida: Não compreendi porque são 40 andares, por semelhança de triângulo meu resultado deu 12 andares.

Xm - 6m

150m - 25m

Xm = 900/25 = 36 metros, sendo cada andar 3 metros, temos 12 andares (??)

por Arlindocampos07 Sáb 07 maio 2022, 16:19

Olá! Você poderia mandar uma foto da sua resolução? Gostaria de entender a semelhança de triângulos que você analisou.

por **Elcioschin** Sáb 07 maio 2022, 16:21

E) Às 8 horas o poste de 6m tem sombra de 7,5 m

6/7,5 = 3.40/x ---> x = 3.40.7,5/6 --> x = 150 m

por Bnlla Dom 08 maio 2022, 19:25

Ainda não compreendi por que utilizar como referência o horário da sombra às 08:00 horas, não poderia ser qualquer um?

por **Elcioschin** Dom 08 maio 2022, 19:32

Teste cada alternativa e vc verá que somente na E se chega ao valor 150

por Arlindocampos07 Dom 08 maio 2022, 20:10

Como o mestre Elcio falou, basta ir testando as alternativas. Não acredito que esse seja um problema que seja viável recorrer apenas à geometria e tentar chegar a uma resposta, uma vez que há uma grande variação nos valores das sombras.

Uma dica, seria você fazer o seguinte: Olha os horários que estão sendo colocados em cada alternativa, olha o tamanho da sombra do poste nesse horário, e faz a relação com o número de andares que faria sombra (150m) nesse mesmo horário. Exemplo:

a) 12 andares gerará sombra na praia até as 10:00.

[latex]\\2\; andares\; ----\; 3\; metros\, (de\: sombra)\\x\; andares\; ----\; 150\; metros\, (de\: sombra)\\\\x=100\; andares,\; logo,\; letra\; a)\; est\acute{a}\; errada.[/latex]

Faça isso com todas as outras alternativas e veja que apenas a letra e) irá dar um número correto de andares para o determinado horário.