Bizu Teorema de Menelaus e Teorema de Ceva
4 participantes
Página 1 de 1
 Bizu Teorema de Menelaus e Teorema de Ceva
Bizu Teorema de Menelaus e Teorema de Ceva
Fala, pessoal.
Vou deixar aqui um tópico especial sobre dois teoremas muito fortes em relações métricas: o teorema de Menelaus e o teorema de Ceva. Tem um bizu muito forte que facilita a memorização, mas antes vou demonstrá-los:
I) Teorema de Menelaus:
Pense nesse teorema sempre que deseje analisar colinearidade de pontos:

Seja o triângulo ABC cortado pela reta FD na qual sua interseção com AB é E.
Se F, E e D são colineares, vale o teorema de Menelaus.
Primeiro, construa BP paralelo a AC.
Assim, perceba que ∆BPD e o ∆FDC são semelhantes:
[latex]\frac{CD}{FC} = \frac{BD}{BP} -> \frac{FC}{CD}.\frac{BD}{BP}=1[/latex]
∆BPE e o ∆FAE também são semelhantes:
[latex]\frac{FA}{AE} = \frac{BP}{EB} -> \frac{AE}{FA}.\frac{BP}{EB} = 1[/latex]
Multiplicando as duas igualdades, chegamos no teorema:
[latex]\frac{AE}{FA}.\frac{BD}{EB}.\frac{FC}{CD} = 1[/latex]
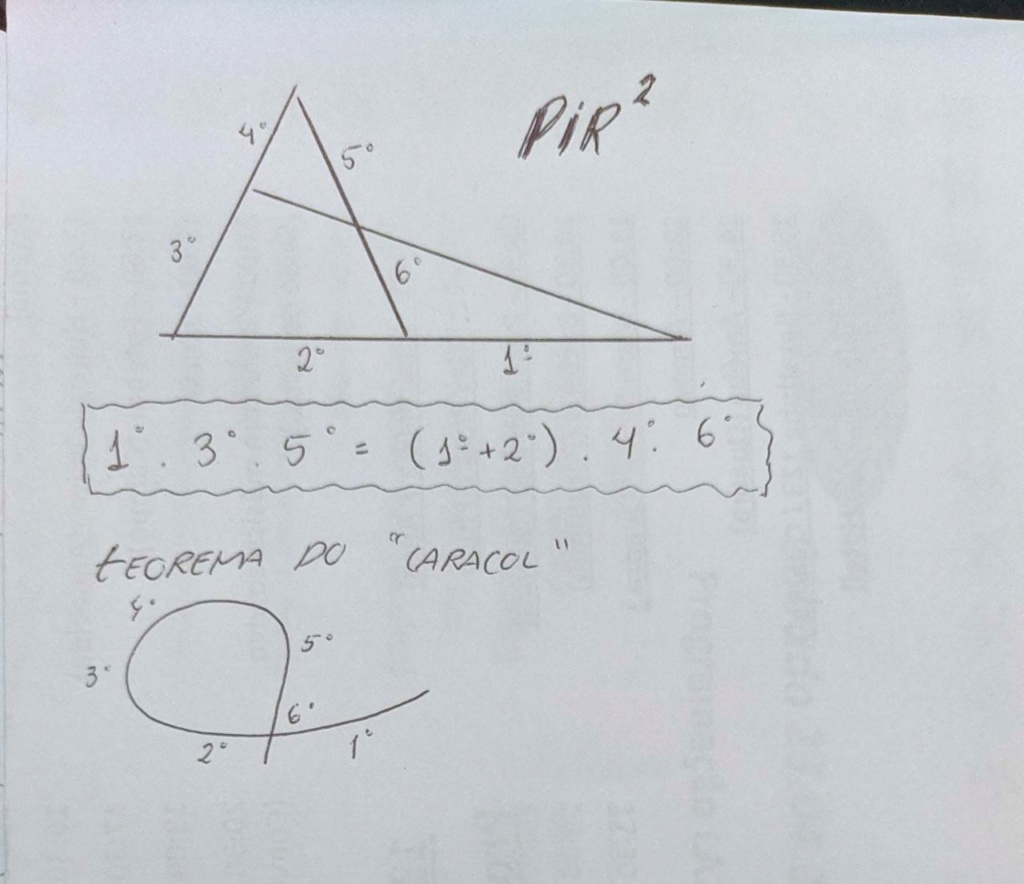
Parece difícil de decorar, então para facilitar sua memorização é só pensar no seguinte:

Marque os vértices do triângulo com bolinhas e os pontos das retas com quadradinhos. Daí siga essa lógica: Comece em uma bolinha, toda bolinha vai para um quadradinho, todo quadradinho vai para uma bolinha e você não pode voltar para um quadradinho ou bolinha já visitado. Isso funciona para qualquer bolinha ou quadradinho escolhido, vou fazer um exemplo para testar:
Começando de A e indo para F:
[latex]AF[/latex]
De F só posso ir para C:
[latex]\frac{AF}{FC}[/latex]
De C tenho que ir para um quadrado, como F já foi vou para D:
[latex]\frac{AF}{FC}.\frac{CD}{}[/latex]
De D eu só posso ir para a bolinha B:
[latex]\frac{AF}{FC}.\frac{CD}{BD}.\frac{}{}[/latex]
De B eu vou para o quadrado E:
[latex]\frac{AF}{FC}.\frac{CD}{BD}.\frac{BE}{}[/latex]
Depois finalizo em A:
[latex]\frac{AF}{FC}.\frac{CD}{BD}.\frac{BE}{EA} = 1[/latex]
Repare que essa igualdade é equivalente à igualdade que encontramos anteriormente. Tente fazer outros casos começando de bolinhas diferentes e compare seu resultado para se familiarizar.
II) Teorema de Ceva:
Pense nesse teorema sempre que quiser analisar interseção de cevianas:

Se as cevianas se intersectam em P vale o teorema de Ceva.
Para demonstrá-lo é simples, basta aplicar o teorema de Menelaus em ACD cortado por BE (i) e ADB cortado por CF (ii).
(i): [latex]\frac{AE}{EC}.\frac{CB}{BD}.\frac{DP}{PA} = 1[/latex]
(ii): [latex]\frac{AP}{PD}.\frac{DC}{CB}.\frac{BF}{FA} = 1[/latex]
Multiplicando (i) e (ii), temos o teorema de Ceva:
[latex]\frac{AE}{EC}.\frac{DC}{BD}.\frac{BF}{FA}=1[/latex]
De novo, para memorizar basta fazer o mesmo desenho dos quadradinhos e das bolinhas:

A única diferença é que não podemos passar pelo ponto P. Daí, começando de C e indo para D:
[latex]CD[/latex]
Depois de D vamos para a bola B:
[latex]\frac{CD}{DB}[/latex]
De B para F:
[latex]\frac{CD}{DB}.\frac{BF}{}[/latex]
De F para A:
[latex]\frac{CD}{DB}.\frac{BF}{FA}[/latex]
De A para E:
[latex]\frac{CD}{DB}.\frac{BF}{FA}.\frac{AE}{}[/latex]
De E para C:
[latex]\frac{CD}{DB}.\frac{BF}{FA}.\frac{AE}{EC} = 1[/latex]
Agora só basta aplicar
Vou deixar aqui um tópico especial sobre dois teoremas muito fortes em relações métricas: o teorema de Menelaus e o teorema de Ceva. Tem um bizu muito forte que facilita a memorização, mas antes vou demonstrá-los:
I) Teorema de Menelaus:
Pense nesse teorema sempre que deseje analisar colinearidade de pontos:

Seja o triângulo ABC cortado pela reta FD na qual sua interseção com AB é E.
Se F, E e D são colineares, vale o teorema de Menelaus.
Primeiro, construa BP paralelo a AC.
Assim, perceba que ∆BPD e o ∆FDC são semelhantes:
[latex]\frac{CD}{FC} = \frac{BD}{BP} -> \frac{FC}{CD}.\frac{BD}{BP}=1[/latex]
∆BPE e o ∆FAE também são semelhantes:
[latex]\frac{FA}{AE} = \frac{BP}{EB} -> \frac{AE}{FA}.\frac{BP}{EB} = 1[/latex]
Multiplicando as duas igualdades, chegamos no teorema:
[latex]\frac{AE}{FA}.\frac{BD}{EB}.\frac{FC}{CD} = 1[/latex]
Parece difícil de decorar, então para facilitar sua memorização é só pensar no seguinte:

Marque os vértices do triângulo com bolinhas e os pontos das retas com quadradinhos. Daí siga essa lógica: Comece em uma bolinha, toda bolinha vai para um quadradinho, todo quadradinho vai para uma bolinha e você não pode voltar para um quadradinho ou bolinha já visitado. Isso funciona para qualquer bolinha ou quadradinho escolhido, vou fazer um exemplo para testar:
Começando de A e indo para F:
[latex]AF[/latex]
De F só posso ir para C:
[latex]\frac{AF}{FC}[/latex]
De C tenho que ir para um quadrado, como F já foi vou para D:
[latex]\frac{AF}{FC}.\frac{CD}{}[/latex]
De D eu só posso ir para a bolinha B:
[latex]\frac{AF}{FC}.\frac{CD}{BD}.\frac{}{}[/latex]
De B eu vou para o quadrado E:
[latex]\frac{AF}{FC}.\frac{CD}{BD}.\frac{BE}{}[/latex]
Depois finalizo em A:
[latex]\frac{AF}{FC}.\frac{CD}{BD}.\frac{BE}{EA} = 1[/latex]
Repare que essa igualdade é equivalente à igualdade que encontramos anteriormente. Tente fazer outros casos começando de bolinhas diferentes e compare seu resultado para se familiarizar.
II) Teorema de Ceva:
Pense nesse teorema sempre que quiser analisar interseção de cevianas:

Se as cevianas se intersectam em P vale o teorema de Ceva.
Para demonstrá-lo é simples, basta aplicar o teorema de Menelaus em ACD cortado por BE (i) e ADB cortado por CF (ii).
(i): [latex]\frac{AE}{EC}.\frac{CB}{BD}.\frac{DP}{PA} = 1[/latex]
(ii): [latex]\frac{AP}{PD}.\frac{DC}{CB}.\frac{BF}{FA} = 1[/latex]
Multiplicando (i) e (ii), temos o teorema de Ceva:
[latex]\frac{AE}{EC}.\frac{DC}{BD}.\frac{BF}{FA}=1[/latex]
De novo, para memorizar basta fazer o mesmo desenho dos quadradinhos e das bolinhas:

A única diferença é que não podemos passar pelo ponto P. Daí, começando de C e indo para D:
[latex]CD[/latex]
Depois de D vamos para a bola B:
[latex]\frac{CD}{DB}[/latex]
De B para F:
[latex]\frac{CD}{DB}.\frac{BF}{}[/latex]
De F para A:
[latex]\frac{CD}{DB}.\frac{BF}{FA}[/latex]
De A para E:
[latex]\frac{CD}{DB}.\frac{BF}{FA}.\frac{AE}{}[/latex]
De E para C:
[latex]\frac{CD}{DB}.\frac{BF}{FA}.\frac{AE}{EC} = 1[/latex]
Agora só basta aplicar
João Pedro Lima- Jedi

- Mensagens : 220
Data de inscrição : 02/01/2022
Idade : 22
Localização : Rio de Janeiro, RJ
Medeiros, gabriel de castro, castelo_hsi, Jvictors021, Arlindocampos07 e Souzz gostam desta mensagem
 Re: Bizu Teorema de Menelaus e Teorema de Ceva
Re: Bizu Teorema de Menelaus e Teorema de Ceva
João, caramba, tô sem palavras. Bizu mais que incrível, nem sei como agradecer. Muito obrigado mesmo, mostrei até para os meus amigos aqui.
Safou demais! Vibrei muito, agradecido pela ajuda.
Safou demais! Vibrei muito, agradecido pela ajuda.

castelo_hsi- Mestre Jedi

- Mensagens : 625
Data de inscrição : 27/06/2021
Localização : São Paulo - SP
João Pedro Lima gosta desta mensagem
 Re: Bizu Teorema de Menelaus e Teorema de Ceva
Re: Bizu Teorema de Menelaus e Teorema de Ceva
Caramba, João.
Transcendeu, simplesmente excelente o bizu!!!
Transcendeu, simplesmente excelente o bizu!!!

scofield- Recebeu o sabre de luz

- Mensagens : 126
Data de inscrição : 08/10/2020
Localização : Brasília
João Pedro Lima gosta desta mensagem
 Re: Bizu Teorema de Menelaus e Teorema de Ceva
Re: Bizu Teorema de Menelaus e Teorema de Ceva
Disponha, rapaziada.
Bons estudos para vocês!
Bons estudos para vocês!
João Pedro Lima- Jedi

- Mensagens : 220
Data de inscrição : 02/01/2022
Idade : 22
Localização : Rio de Janeiro, RJ
castelo_hsi gosta desta mensagem

Jvictors021- Estrela Dourada

- Mensagens : 1116
Data de inscrição : 02/07/2021
Idade : 21
Localização : Passa Quatro - MG
castelo_hsi e João Pedro Lima gostam desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» Teorema de Menelaus ou de Ceva (TALVEZ)
» Teorema de Ceva
» Teorema de Menelaus
» Teorema de Ceva
» Teorema de Menelaus, duvida na proporção
» Teorema de Ceva
» Teorema de Menelaus
» Teorema de Ceva
» Teorema de Menelaus, duvida na proporção
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos