Teorema de Menelaus ou de Ceva (TALVEZ)
3 participantes
Página 1 de 1
Teorema de Menelaus ou de Ceva (TALVEZ)
por marceloc3lo Qua 17 Mar 2021, 20:43
Fala, galera.
Encontrei o seguinte problema em um livro, mas não consegui solução. Alguém me dá uma luz aí.
b1. b2, b3 e b4 são os lados.
x, y, 3, 2 e 4 são as áreas.
O objetivo é determinar x e y.
Encontrei o seguinte problema em um livro, mas não consegui solução. Alguém me dá uma luz aí.
b1. b2, b3 e b4 são os lados.
x, y, 3, 2 e 4 são as áreas.
O objetivo é determinar x e y.
Última edição por marceloc3lo em Qui 18 Mar 2021, 15:54, editado 1 vez(es)
marceloc3lo- Iniciante
- Mensagens : 1
Data de inscrição : 17/03/2021
Re: Teorema de Menelaus ou de Ceva (TALVEZ)
por Vitor Ahcor Qua 17 Mar 2021, 21:29
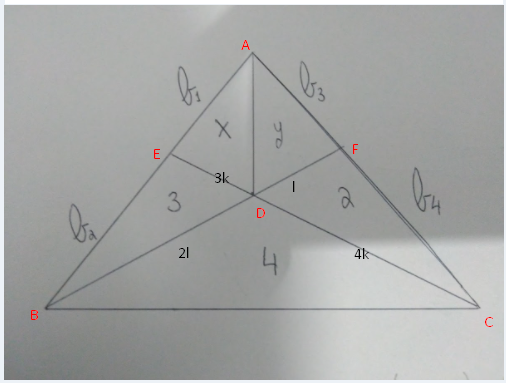
Fato utilizado: Se dois triângulos compartilham a mesma altura, então suas áreas serão proporcionais as suas respectivas bases. Sendo assim:
(i) [BCD]/ BD = [CDF]/ DF .: 4/BD = 2/DF .: BD = 2 DF.
(ii) [ABD]/BD = [ADF]/DF .: (x+3)/2 = y/1 .: x+3 = 2y (*)
(iii) [BDE]/DE = [BCD]/CD .: 3/DE = 4/CD .: 4DE = 3 CD
(iv) [AED]/DE = [ACD]/CD .: x/3 = (y+2)/4 .: 4x = 3y + 6 (**)
De (*) e (**) obtemos x = 21/5 e y = 18/5.
____________________________________________
Cha-la head-cha-la
Vitor Ahcor- Monitor
- Mensagens : 780
Data de inscrição : 21/12/2018
Idade : 24
Localização : Taurdal
Medeiros gosta desta mensagem
Re: Teorema de Menelaus ou de Ceva (TALVEZ)
por Medeiros Qui 18 Mar 2021, 00:22
gostei muito da resolução do Vitor. Tenho ideia para fazer a mesma coisa por um caminho ligeiramente diferente.
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Vitor Ahcor gosta desta mensagem
Re: Teorema de Menelaus ou de Ceva (TALVEZ)
por Vitor Ahcor Qui 18 Mar 2021, 09:18
Gostei Medeiros, assim fica + elegante a solução ..
____________________________________________
Cha-la head-cha-la
Vitor Ahcor- Monitor
- Mensagens : 780
Data de inscrição : 21/12/2018
Idade : 24
Localização : Taurdal
Tópicos semelhantes» Bizu Teorema de Menelaus e Teorema de Ceva
» TEOREMA DE CEVA
» Teorema de Ceva
» Teorema de Ceva
» Teorema de Menelaus, duvida na proporção
» TEOREMA DE CEVA
» Teorema de Ceva
» Teorema de Ceva
» Teorema de Menelaus, duvida na proporção
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
