Sistemas SPD , SPI e SI
2 participantes
Página 1 de 1
 Sistemas SPD , SPI e SI
Sistemas SPD , SPI e SI
A respeito de matrizes, determinantes e sistemas lineares é correto afirmar que:
Alternativas
A)Se A é uma matriz quadrada, então [latex]det(A) = \frac{1}{(det(A^{T}))}[/latex]
B)Se
C)Se A é uma matriz e r ∈ |R* então [latex](rA)^{T} =\frac{ 1}{rA^{T}}[/latex] ;
D)O sistema é possível e indeterminado;
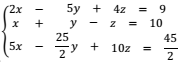
E)Dois sistemas lineares só podem ser equivalentes se forem ambos possíveis e determinados.
Na alternativa D montei um sistema igual o abaixo e descobri seu determinante:
[latex]\begin{bmatrix} 2 & -5 & 4 \\ 1& 1 &-1 \\ 5& -25/2 &10 & \end{bmatrix}[/latex]
Descobri que o Determinante é igual a 0.
Das minhas anotações tenho que quando o Det = 0 então o Sistema pode ser SPI ou SI.
Minha dúvida é a seguinte: agora que descobri que o determinante é 0, como faço para saber se o sistema é SI ou SPI?
Alternativas
A)Se A é uma matriz quadrada, então [latex]det(A) = \frac{1}{(det(A^{T}))}[/latex]
B)Se

C)Se A é uma matriz e r ∈ |R* então [latex](rA)^{T} =\frac{ 1}{rA^{T}}[/latex] ;
D)O sistema é possível e indeterminado;
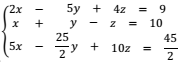
E)Dois sistemas lineares só podem ser equivalentes se forem ambos possíveis e determinados.
- Spoiler:
- Resposta:D
Na alternativa D montei um sistema igual o abaixo e descobri seu determinante:
[latex]\begin{bmatrix} 2 & -5 & 4 \\ 1& 1 &-1 \\ 5& -25/2 &10 & \end{bmatrix}[/latex]
Descobri que o Determinante é igual a 0.
Das minhas anotações tenho que quando o Det = 0 então o Sistema pode ser SPI ou SI.
Minha dúvida é a seguinte: agora que descobri que o determinante é 0, como faço para saber se o sistema é SI ou SPI?
Última edição por samuelbelembr@gmail.com em Seg 18 Abr 2022, 11:11, editado 1 vez(es)
samuelbelembr@gmail.com- Jedi

- Mensagens : 205
Data de inscrição : 04/10/2021
 Re: Sistemas SPD , SPI e SI
Re: Sistemas SPD , SPI e SI
Olá Samuel;
O próximo passo é escalonar a matriz, nesse processo, você vai encontrar uma equação assim: 0 = 0. Essa linha (equação) pode ser desconsiderada do sistema, assim ficamos com 2 equações lineares e 3 incógnitas, dessa forma, temos um caso de SPI. Se no caso você escalonasse a matriz e encontrasse algo do tipo: 0 = 1, ou qualquer outro resultado absurdo, teríamos SI. Tente desenvolver, se não conseguir eu te dou uma mão.
O próximo passo é escalonar a matriz, nesse processo, você vai encontrar uma equação assim: 0 = 0. Essa linha (equação) pode ser desconsiderada do sistema, assim ficamos com 2 equações lineares e 3 incógnitas, dessa forma, temos um caso de SPI. Se no caso você escalonasse a matriz e encontrasse algo do tipo: 0 = 1, ou qualquer outro resultado absurdo, teríamos SI. Tente desenvolver, se não conseguir eu te dou uma mão.
____________________________________________
Dê tempo ao
Lateralus Φ

qedpetrich- Monitor

- Mensagens : 2498
Data de inscrição : 05/07/2021
Idade : 24
Localização : Erechim - RS / Passo Fundo - RS
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













