FME - Inequação Modular
4 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 FME - Inequação Modular
FME - Inequação Modular
(Q.389 - letra e) Resolva as inequações em R.
[latex]\frac{2x-3}{\left | 3x-1 \right |}>2[/latex]
Gabarito do livro: (Imagens abaixo)

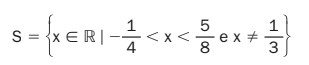
A forma que eu fiz foi
1º) Fiz a condição para o denominador, daí vem x≠ 1/3
2º) Resolvi a inequação normalmente, aplicando a teoria "|x|>k <-----> x<-k ou x>k"
3º) Encontrei que x<-1/4 ou x<5/8
Ao comparar a minha resolução com a do livro, fiquei na dúvida se o fato de ele ter aplicado o módulo na fração inteira e resolvido a inequação foi por erro de digitação ou se realmente foi um artifício que o autor usou. Se foi, alguém poderia me explicar? Muito obrigada pela ajuda
[latex]\frac{2x-3}{\left | 3x-1 \right |}>2[/latex]
Gabarito do livro: (Imagens abaixo)

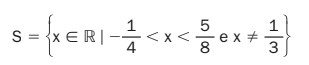
A forma que eu fiz foi
1º) Fiz a condição para o denominador, daí vem x≠ 1/3
2º) Resolvi a inequação normalmente, aplicando a teoria "|x|>k <-----> x<-k ou x>k"
3º) Encontrei que x<-1/4 ou x<5/8
Ao comparar a minha resolução com a do livro, fiquei na dúvida se o fato de ele ter aplicado o módulo na fração inteira e resolvido a inequação foi por erro de digitação ou se realmente foi um artifício que o autor usou. Se foi, alguém poderia me explicar? Muito obrigada pela ajuda
victoria-rios-2001- Iniciante
- Mensagens : 19
Data de inscrição : 07/04/2021
Idade : 23
Kaik gosta desta mensagem
 Re: FME - Inequação Modular
Re: FME - Inequação Modular
A solução do seu livro está correta.
Você só pode aplicar o módulo no denominador.
Você só pode aplicar o módulo no denominador.

Elcioschin- Grande Mestre

- Mensagens : 73174
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
qedpetrich gosta desta mensagem
 Re: FME - Inequação Modular
Re: FME - Inequação Modular
Então mestre, mas tô confusa porque se eu só posso aplicar o módulo no denominador, pq o livro aplicou na fração inteira?
victoria-rios-2001- Iniciante
- Mensagens : 19
Data de inscrição : 07/04/2021
Idade : 23
qedpetrich e JUJUBA_SAMA gostam desta mensagem
 Re: FME - Inequação Modular
Re: FME - Inequação Modular
Foi aplicado a definição modular em seguida resolvido as duas inequações, o livro foi direto nos intervalos que contemplam as soluções, eu resolveria pelo método quadro-quociente, vou fazer a primeira depois você faz analogamente para os valores maiores que dois.
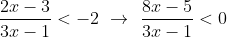
Quadro-quociente:
8x - 5 - - - - - - - - - - - - - - [ 5/8 ] + + + + + +
3x - 1 - - - - [ 1/3 ] + + + + + + + + + + + + +
(8x-5)/(3x-1) + + + [ 1/3 ] - - - - - [ 5/8 ] + + + + + +
O intervalo definido é:
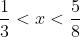
Sua solução está incompleta, você apenas considerou o numerador, deve ser levado em consideração o denominador também!
Ficou claro dessa forma? Espero ter ajudado!
Quadro-quociente:
8x - 5 - - - - - - - - - - - - - - [ 5/8 ] + + + + + +
3x - 1 - - - - [ 1/3 ] + + + + + + + + + + + + +
(8x-5)/(3x-1) + + + [ 1/3 ] - - - - - [ 5/8 ] + + + + + +
O intervalo definido é:
Sua solução está incompleta, você apenas considerou o numerador, deve ser levado em consideração o denominador também!
Ficou claro dessa forma? Espero ter ajudado!
____________________________________________
Dê tempo ao
Lateralus Φ

qedpetrich- Monitor

- Mensagens : 2498
Data de inscrição : 05/07/2021
Idade : 24
Localização : Erechim - RS / Passo Fundo - RS
 Re: FME - Inequação Modular
Re: FME - Inequação Modular
Muito obrigada!!! Me ajudou sim 



victoria-rios-2001- Iniciante
- Mensagens : 19
Data de inscrição : 07/04/2021
Idade : 23
qedpetrich gosta desta mensagem
 Re: FME - Inequação Modular
Re: FME - Inequação Modular
Mestre, eu também travei nessa questão pois no livro só o denominador está em módulo e na resolução a fração inteira está em módulo.Elcioschin escreveu:A solução do seu livro está correta.
Você só pode aplicar o módulo no denominador.
Pablo Willamys- Iniciante
- Mensagens : 24
Data de inscrição : 22/10/2022
Idade : 20
Localização : Camocim-CE
 Re: FME - Inequação Modular
Re: FME - Inequação Modular
Foi apenas um erro do próprio livro, considere o módulo tanto no numerador quanto no denominador!
____________________________________________
Dê tempo ao
Lateralus Φ

qedpetrich- Monitor

- Mensagens : 2498
Data de inscrição : 05/07/2021
Idade : 24
Localização : Erechim - RS / Passo Fundo - RS
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












