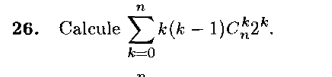Binômio de Newton
2 participantes
Página 1 de 1
 Re: Binômio de Newton
Re: Binômio de Newton
Tomando a função f(x):
[latex]f(x) = \sum_{k=0}^{n}k\cdot (k-1)\cdot \binom{n}{k}\cdot x^k[/latex]
Como K=0 e k=1 dão números nulos:
[latex]f(x) = \sum_{k=2}^{n}k\cdot (k-1)\cdot \binom{n}{k}\cdot x^k[/latex]
[latex]f(x) = \sum_{k=0}^{n-2}(k+2)\cdot (k+1)\cdot \binom{n}{k+2}\cdot x^{k+2}[/latex]
[latex]f(x) = x^{2}\cdot \left [\sum_{k=0}^{n-2}\binom{n}{k+2}\cdot (k+2)\cdot (k+1)\cdot x^{k} \right ][/latex]
[latex]f(x) = x^{2}\cdot \left [\sum_{k=0}^{n-2}\binom{n}{k+2}\cdot \frac{\mathrm{d^2} x^{k+2}}{\mathrm{d} x^2} \right ][/latex]
Jogando o somatório para dentro da derivada, já que ele é constante em relação a x,
[latex]f(x) = x^{2}\cdot \frac{\mathrm{d^2} \left (\sum_{k=0}^{n-2}\binom{n}{k+2}\cdot x^{k+2} \right )}{\mathrm{d} x^2}[/latex]
[latex]f(x) = x^{2}\cdot \frac{\mathrm{d^2} \left (\sum_{k=2}^{n}\binom{n}{k}\cdot x^{k} \right )}{\mathrm{d} x^2}[/latex]
[latex]f(x) = x^{2}\cdot \frac{\mathrm{d^2} \left (\sum_{k=0}^{n}\left (\binom{n}{k}\cdot x^{k} \right ) - \binom{n}{1}\cdot x - \binom{n}{0}x^0 \right )}{\mathrm{d} x^2}[/latex]
[latex]f(x) = x^{2}\cdot \left (\frac{\mathrm{d^2} \left (\sum_{k=0}^{n}\binom{n}{k}\cdot x^{k} \right )}{\mathrm{d} x^2} - \frac{\mathrm{d^2} \left (\binom{n}{1}\cdot x \right )}{\mathrm{d} x^2} - \frac{\mathrm{d^2} \left ( \binom{n}{0}x^0 \right )}{\mathrm{d} x^2} \right )[/latex]
[latex]f(x) = x^{2}\cdot \left (\frac{\mathrm{d^2} \left ( \left ( x+1 \right )^n \right )}{\mathrm{d} x^2} - \frac{\mathrm{d^2} \left (x \right )}{\mathrm{d} x^2} - \frac{\mathrm{d^2} \left ( 1 \right )}{\mathrm{d} x^2} \right )[/latex]
[latex]f(x) = x^{2}\cdot \frac{\mathrm{d^2} \left ( \left ( x+1 \right )^n \right )}{\mathrm{d} x^2}[/latex]
[latex]f(x) = x^{2}\cdot \frac{\mathrm{d} \left ( n\left ( x+1 \right )^{n-1} \right )}{\mathrm{d} x}[/latex]
[latex]f(x) = x^{2}\cdot \left ( n\cdot (n-1)\left ( x+1 \right )^{n-2} \right )[/latex]
[latex]f(x) = n\cdot (n-1)\cdot \left (\frac{x}{x+1} \right )^{2}\cdot \left ( x+1 \right )^{n}[/latex]
*Temos, então, que a solução ocorre quando x=2. Logo,
[latex]S = \frac{4\cdot n\cdot (n-1)\cdot 3^{n}}{9}[/latex]
[latex]f(x) = \sum_{k=0}^{n}k\cdot (k-1)\cdot \binom{n}{k}\cdot x^k[/latex]
Como K=0 e k=1 dão números nulos:
[latex]f(x) = \sum_{k=2}^{n}k\cdot (k-1)\cdot \binom{n}{k}\cdot x^k[/latex]
[latex]f(x) = \sum_{k=0}^{n-2}(k+2)\cdot (k+1)\cdot \binom{n}{k+2}\cdot x^{k+2}[/latex]
[latex]f(x) = x^{2}\cdot \left [\sum_{k=0}^{n-2}\binom{n}{k+2}\cdot (k+2)\cdot (k+1)\cdot x^{k} \right ][/latex]
[latex]f(x) = x^{2}\cdot \left [\sum_{k=0}^{n-2}\binom{n}{k+2}\cdot \frac{\mathrm{d^2} x^{k+2}}{\mathrm{d} x^2} \right ][/latex]
Jogando o somatório para dentro da derivada, já que ele é constante em relação a x,
[latex]f(x) = x^{2}\cdot \frac{\mathrm{d^2} \left (\sum_{k=0}^{n-2}\binom{n}{k+2}\cdot x^{k+2} \right )}{\mathrm{d} x^2}[/latex]
[latex]f(x) = x^{2}\cdot \frac{\mathrm{d^2} \left (\sum_{k=2}^{n}\binom{n}{k}\cdot x^{k} \right )}{\mathrm{d} x^2}[/latex]
[latex]f(x) = x^{2}\cdot \frac{\mathrm{d^2} \left (\sum_{k=0}^{n}\left (\binom{n}{k}\cdot x^{k} \right ) - \binom{n}{1}\cdot x - \binom{n}{0}x^0 \right )}{\mathrm{d} x^2}[/latex]
[latex]f(x) = x^{2}\cdot \left (\frac{\mathrm{d^2} \left (\sum_{k=0}^{n}\binom{n}{k}\cdot x^{k} \right )}{\mathrm{d} x^2} - \frac{\mathrm{d^2} \left (\binom{n}{1}\cdot x \right )}{\mathrm{d} x^2} - \frac{\mathrm{d^2} \left ( \binom{n}{0}x^0 \right )}{\mathrm{d} x^2} \right )[/latex]
[latex]f(x) = x^{2}\cdot \left (\frac{\mathrm{d^2} \left ( \left ( x+1 \right )^n \right )}{\mathrm{d} x^2} - \frac{\mathrm{d^2} \left (x \right )}{\mathrm{d} x^2} - \frac{\mathrm{d^2} \left ( 1 \right )}{\mathrm{d} x^2} \right )[/latex]
[latex]f(x) = x^{2}\cdot \frac{\mathrm{d^2} \left ( \left ( x+1 \right )^n \right )}{\mathrm{d} x^2}[/latex]
[latex]f(x) = x^{2}\cdot \frac{\mathrm{d} \left ( n\left ( x+1 \right )^{n-1} \right )}{\mathrm{d} x}[/latex]
[latex]f(x) = x^{2}\cdot \left ( n\cdot (n-1)\left ( x+1 \right )^{n-2} \right )[/latex]
[latex]f(x) = n\cdot (n-1)\cdot \left (\frac{x}{x+1} \right )^{2}\cdot \left ( x+1 \right )^{n}[/latex]
*Temos, então, que a solução ocorre quando x=2. Logo,
[latex]S = \frac{4\cdot n\cdot (n-1)\cdot 3^{n}}{9}[/latex]
MessiasCastro- Iniciante
- Mensagens : 28
Data de inscrição : 22/10/2021
Idade : 26
Localização : Fortaleza, CE. Brasil.
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos