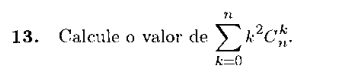Números binomiais
2 participantes
Página 1 de 1
ale2906- Iniciante
- Mensagens : 5
Data de inscrição : 17/10/2021
Re: Números binomiais
por MessiasCastro Ter 16 Nov 2021, 16:31
Bom...
Se Ck,n tem k < n, então Ck,n = 0. Logo,
[latex]{\color{Red} S = \sum_{k=0}^{n}k^2\cdot C_{n}^{k} = n^2\cdot C_{n}^{n} = n^2}[/latex]
Mas não acho que é isso que a questão queria propor. Portanto, farei considerando Cn,k.
I) Tome a função f(x):
[latex]f(x) = \left ( x+1 \right )^{n} = \sum_{k=0}^{n}C_{k}^{n}\cdot x^k[/latex]
*Usando o processo de derivação temos:
[latex]\left\{\begin{matrix} \frac{\mathrm{d} f(x)}{\mathrm{d} x} = \sum_{k=0}^{n}k\cdot C_{k}^{n}\cdot x^{k-1} \\ \\ \frac{\mathrm{d^2} f(x)}{\mathrm{d} x^2} = \sum_{k=0}^{n}k(k-1)\cdot C_{k}^{n}\cdot x^{k-2} \end{matrix}\right.[/latex]
[latex]\left\{\begin{matrix} x\cdot \frac{\mathrm{d} f(x)}{\mathrm{d} x} = \sum_{k=0}^{n}k\cdot C_{k}^{n}\cdot x^{k} \\ \\ x^{2}\cdot \frac{\mathrm{d^2} f(x)}{\mathrm{d} x^2} = \sum_{k=0}^{n}k(k-1)\cdot C_{k}^{n}\cdot x^{k} \end{matrix}\right.[/latex]
*Com isso, percebe-se que:
[latex]x^{2}\cdot \frac{\mathrm{d^2} f(x)}{\mathrm{d} x^2} = \left ( \sum_{k=0}^{n} k^2\cdot c_{k}^{n}\cdot x^{k}\right ) -x\cdot \frac{\mathrm{d} f(x)}{\mathrm{d} x}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n}\cdot x^{k} = x^{2}\cdot \frac{\mathrm{d^2} f(x)}{\mathrm{d} x^2} + x\cdot \frac{\mathrm{d} f(x)}{\mathrm{d} x}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n}\cdot x^{k} = x^{2}\cdot \frac{\mathrm{d^2} \left [\left ( x+1 \right )^n \right ]}{\mathrm{d} x^2} + x\cdot \frac{\mathrm{d} \left [\left ( x+1 \right )^n \right ]}{\mathrm{d} x}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n}\cdot x^{k} = x^{2}\cdot n\cdot (n-1)\cdot (x+1)^{n-2} + x\cdot n\cdot (x+1)^{n-1}[/latex]
*Quando x = 1,
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n}\cdot 1^{k} = 1^{2}\cdot n\cdot (n-1)\cdot (1+1)^{n-2} + 1\cdot n\cdot (1+1)^{n-1}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n} = n\cdot (n-1)\cdot 2^{n-2} + n\cdot 2^{n-1}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n} = \frac{n\cdot (n-1)}{4}\cdot 2^{n} + \frac{n}{2}\cdot 2^{n}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n} = \left (\frac{n^{2} - n}{4} + \frac{n}{2} \right )\cdot 2^{n}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n} = \frac{n^{2} + n}{4}\cdot 2^{n}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n} = \frac{n\cdot (n+1)}{4}\cdot 2^{n}[/latex]
Se Ck,n tem k < n, então Ck,n = 0. Logo,
[latex]{\color{Red} S = \sum_{k=0}^{n}k^2\cdot C_{n}^{k} = n^2\cdot C_{n}^{n} = n^2}[/latex]
Mas não acho que é isso que a questão queria propor. Portanto, farei considerando Cn,k.
I) Tome a função f(x):
[latex]f(x) = \left ( x+1 \right )^{n} = \sum_{k=0}^{n}C_{k}^{n}\cdot x^k[/latex]
*Usando o processo de derivação temos:
[latex]\left\{\begin{matrix} \frac{\mathrm{d} f(x)}{\mathrm{d} x} = \sum_{k=0}^{n}k\cdot C_{k}^{n}\cdot x^{k-1} \\ \\ \frac{\mathrm{d^2} f(x)}{\mathrm{d} x^2} = \sum_{k=0}^{n}k(k-1)\cdot C_{k}^{n}\cdot x^{k-2} \end{matrix}\right.[/latex]
[latex]\left\{\begin{matrix} x\cdot \frac{\mathrm{d} f(x)}{\mathrm{d} x} = \sum_{k=0}^{n}k\cdot C_{k}^{n}\cdot x^{k} \\ \\ x^{2}\cdot \frac{\mathrm{d^2} f(x)}{\mathrm{d} x^2} = \sum_{k=0}^{n}k(k-1)\cdot C_{k}^{n}\cdot x^{k} \end{matrix}\right.[/latex]
*Com isso, percebe-se que:
[latex]x^{2}\cdot \frac{\mathrm{d^2} f(x)}{\mathrm{d} x^2} = \left ( \sum_{k=0}^{n} k^2\cdot c_{k}^{n}\cdot x^{k}\right ) -x\cdot \frac{\mathrm{d} f(x)}{\mathrm{d} x}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n}\cdot x^{k} = x^{2}\cdot \frac{\mathrm{d^2} f(x)}{\mathrm{d} x^2} + x\cdot \frac{\mathrm{d} f(x)}{\mathrm{d} x}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n}\cdot x^{k} = x^{2}\cdot \frac{\mathrm{d^2} \left [\left ( x+1 \right )^n \right ]}{\mathrm{d} x^2} + x\cdot \frac{\mathrm{d} \left [\left ( x+1 \right )^n \right ]}{\mathrm{d} x}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n}\cdot x^{k} = x^{2}\cdot n\cdot (n-1)\cdot (x+1)^{n-2} + x\cdot n\cdot (x+1)^{n-1}[/latex]
*Quando x = 1,
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n}\cdot 1^{k} = 1^{2}\cdot n\cdot (n-1)\cdot (1+1)^{n-2} + 1\cdot n\cdot (1+1)^{n-1}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n} = n\cdot (n-1)\cdot 2^{n-2} + n\cdot 2^{n-1}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n} = \frac{n\cdot (n-1)}{4}\cdot 2^{n} + \frac{n}{2}\cdot 2^{n}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n} = \left (\frac{n^{2} - n}{4} + \frac{n}{2} \right )\cdot 2^{n}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n} = \frac{n^{2} + n}{4}\cdot 2^{n}[/latex]
[latex]\sum_{k=0}^{n} k^2\cdot c_{k}^{n} = \frac{n\cdot (n+1)}{4}\cdot 2^{n}[/latex]
MessiasCastro- Iniciante
- Mensagens : 28
Data de inscrição : 22/10/2021
Idade : 26
Localização : Fortaleza, CE. Brasil.
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
