Equações Algébricas
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Equações Algébricas
Equações Algébricas
Olá! Não estou conseguindo encontrar as raízes ..
Uma ajuda no item a) será de grande valia.
(Fuvest- Não sei ano) A equação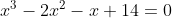 tem uma raiz inteira r e duas imaginárias s e t.
tem uma raiz inteira r e duas imaginárias s e t.
a) Determine as raízes r, s e t.
b) Escreva a equação cujas raízes são 1/r, 1/t e 1/s.
c) Determine a equação cujas raízes são st, rs e rt.
Obrigado!
Uma ajuda no item a) será de grande valia.
(Fuvest- Não sei ano) A equação
a) Determine as raízes r, s e t.
b) Escreva a equação cujas raízes são 1/r, 1/t e 1/s.
c) Determine a equação cujas raízes são st, rs e rt.
Obrigado!
Jessé de Jesus- Recebeu o sabre de luz

- Mensagens : 153
Data de inscrição : 26/08/2011
Idade : 31
Localização : Ubatuba
 Re: Equações Algébricas
Re: Equações Algébricas
x³ - 2x² - x + 14 = 0
a) Pesquisa de raízes racionais (divisores inteiros de 14): - 14, -7, -2, -1 +1, +2, +7, +14
Testando ---> r = -2 é uma raiz
Briott-Ruffini
__|1 ... - 2 ... - 1 ... 14
-2|1 ... -4 ...... 7 ..... 0
b) Demais raízes ---->
x² - 4x + 7 = 0 ---> Discriminante: D = (-4)² - 4*1*7 ----> D = -12
x = (4 + - i*2*\/3)/2*1 ----> s = 2 + i*\/3 ---> t = 2 - i*\/3
1/r = 1/-2 ----> 1/r = -1/2
1/s = 1/(2 + i*\/3) ----> 1/s = (2 - i*\/3)/(4 + 3) ----> 1/s = 2/7 - i*\/3/7
1/t = 1/(2 - i*\/3) -----> 1/t = (2 + i*\/3)/(4 + 3) ----> 1/t = 2/7 - i*\/3/7
Relações de Girard
1/r + 1/s + 1/t = - b/a ----> - 1/2 + (2/7 - i*\/3/7) + (2 + i*\/3/7) = -b/a ----> - b/a = 1/14 ---> b = - a/14 ----> I
(1/r)*(1/s) + (1/r)*(1/t) + (1/s)*(1/t = c/a ----> (-1/2)*(2/7 - i*\/3/7) + (-1/2)*(2/7 + i*\/3/7) + (2/7 + i*\/3/7)*(2/7 - i*\/3/7)
Faça contas e calcule c/a
(1/r)*1/s)*(1/t) = - d/a ---> Calcule d/a
c) Faça o mesmo para as raízes st, rs, e rt
a) Pesquisa de raízes racionais (divisores inteiros de 14): - 14, -7, -2, -1 +1, +2, +7, +14
Testando ---> r = -2 é uma raiz
Briott-Ruffini
__|1 ... - 2 ... - 1 ... 14
-2|1 ... -4 ...... 7 ..... 0
b) Demais raízes ---->
x² - 4x + 7 = 0 ---> Discriminante: D = (-4)² - 4*1*7 ----> D = -12
x = (4 + - i*2*\/3)/2*1 ----> s = 2 + i*\/3 ---> t = 2 - i*\/3
1/r = 1/-2 ----> 1/r = -1/2
1/s = 1/(2 + i*\/3) ----> 1/s = (2 - i*\/3)/(4 + 3) ----> 1/s = 2/7 - i*\/3/7
1/t = 1/(2 - i*\/3) -----> 1/t = (2 + i*\/3)/(4 + 3) ----> 1/t = 2/7 - i*\/3/7
Relações de Girard
1/r + 1/s + 1/t = - b/a ----> - 1/2 + (2/7 - i*\/3/7) + (2 + i*\/3/7) = -b/a ----> - b/a = 1/14 ---> b = - a/14 ----> I
(1/r)*(1/s) + (1/r)*(1/t) + (1/s)*(1/t = c/a ----> (-1/2)*(2/7 - i*\/3/7) + (-1/2)*(2/7 + i*\/3/7) + (2/7 + i*\/3/7)*(2/7 - i*\/3/7)
Faça contas e calcule c/a
(1/r)*1/s)*(1/t) = - d/a ---> Calcule d/a
c) Faça o mesmo para as raízes st, rs, e rt

Elcioschin- Grande Mestre

- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Equações Algébricas
Re: Equações Algébricas
Obrigado!
Não tinha entendido direito o Teorema das raízes racionais, aí não deu para fazer...
Encontrei um jeito mais rápido para fazer os itens b) e c) :
b) Façamos uma equação transformada com a seguinte lei: y=1/x, logo x=1/y. Daí:
^3-2\left ( 1/y \right )^2-\left ( 1/y \right )+14=0)
Desenvolvendo...
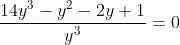
A equação será: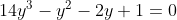
c) st, rs e rt podem ser escritos rst/r, rst/t e rts/s. Pelas Relações de Girard.. rst=-14. Farei o mesmo que no item anterior com a transformada g=-14/x, que também satisfaz x=-14/g. Aí..
^3-2\left ( \frac{-14}{g} \right )^2-\left ( \frac{-14}{g} \right )+14=0)
E a equação: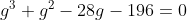
Não tinha entendido direito o Teorema das raízes racionais, aí não deu para fazer...
Encontrei um jeito mais rápido para fazer os itens b) e c) :
b) Façamos uma equação transformada com a seguinte lei: y=1/x, logo x=1/y. Daí:
Desenvolvendo...
A equação será:
c) st, rs e rt podem ser escritos rst/r, rst/t e rts/s. Pelas Relações de Girard.. rst=-14. Farei o mesmo que no item anterior com a transformada g=-14/x, que também satisfaz x=-14/g. Aí..
E a equação:
Jessé de Jesus- Recebeu o sabre de luz

- Mensagens : 153
Data de inscrição : 26/08/2011
Idade : 31
Localização : Ubatuba
 Tópicos semelhantes
Tópicos semelhantes» Equações Algébricas
» Equações algébricas
» Equações algébricas
» Equações Algébricas
» Equações algébricas
» Equações algébricas
» Equações algébricas
» Equações Algébricas
» Equações algébricas
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












