inequação modular

Resolva: |2x-4| - |x+1| + 3x >= 0

|2x-4| --> 2x-4, se x >= 2
                -2x+4, se x < 2
|x+1| --> x+1, se x >= -1
               -x-1, se x < -1

Analisando os intervalos:

                | (-inf,-1[  -1  [-1,2]  2   [2,+inf)
|2x-4| --> |  -2x+4    |  -2x+4   |     2x-4
|x+1| -->  |   -x-1      |    x+1    |     x+1

I) se x<-1 --> -2x+4+x+1+3x >= 0 --> x >= -5/2 --> S'=(-inf,-1[ interseção [-5/2,+inf) --> S'=[-5/2,-1) --> Obs.: Porque deve ser interseção aqui?
II) se -1<=x<2 --> -2x+4-x-1+3x >= 0 --> x >= 0 --> absurdo --> S"={} interseção [-1,2] --> S"'={}
III) se x>=2 --> 2x-4-x-1+3x >= 0 --> x >= 5/4 --> S"'=[2,+inf) interseção [5/4,+inf) --> S"'= [2,+inf)

S = S' U S" U S"' = [-5/2,-1) U {} U [2,+inf) --> S = [-5/2,-1) U [2,+inf) --> E porque deve ser união aqui? 
Gabarito = (-5/2,+inf)

Onde estou errando?

Cheguei neste resultado: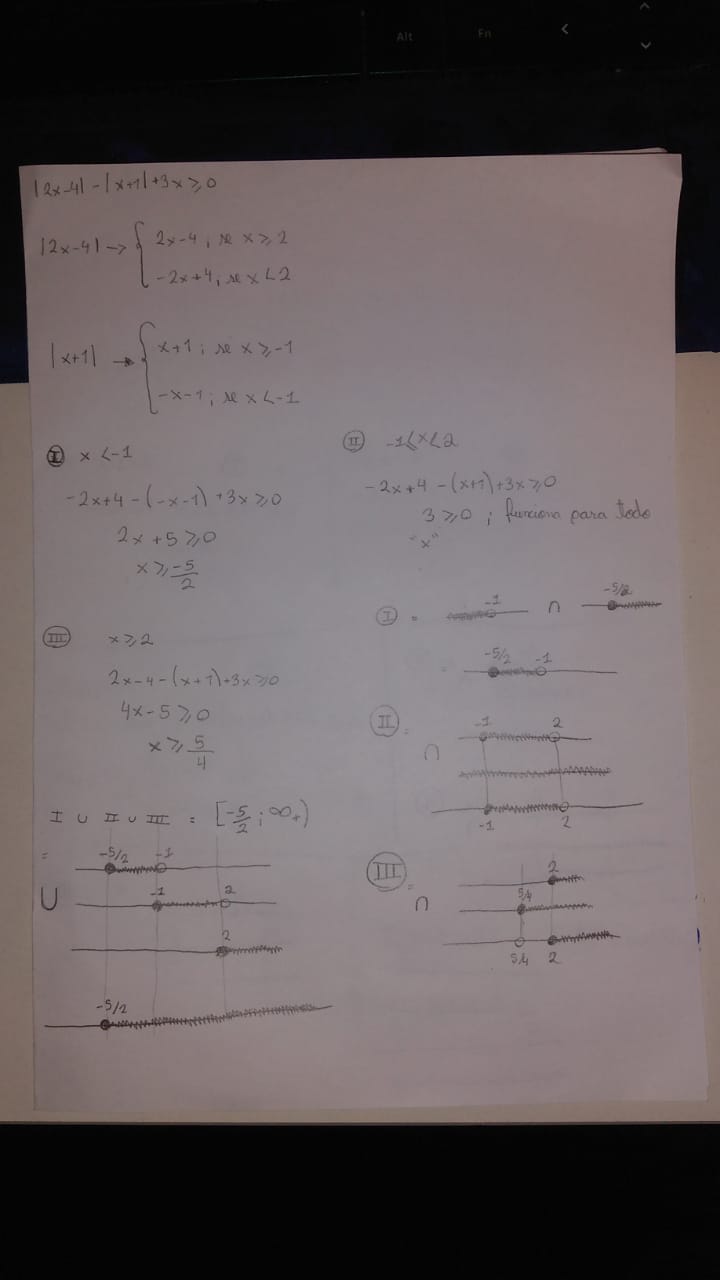



Responderei as suas dúvidas em ordem :

1--- "I) se x<-1 --> -2x+4+x+1+3x >= 0 --> x >= -5/2 --> S'=(-inf,-1[ interseção [-5/2,+inf) --> S'=[-5/2,-1) --> Obs.: Porque deve ser interseção aqui?"
     
         - Deve-se utilizar a intersecção neste caso, pois estamos dizendo que x é necessariamente menor que -1, assim é uma condição de existência para que possamos extrair o módulo nas condições propostas anteriormente, como  por exemplo, extrair o módulo de x+1 na forma -x-1, chegando no resultado final como x sendo maior ou igual a -5/2. Logo, deve-se buscar a intersecção entre elas, pois desejamos que as duas ocorram ao mesmo tempo.

2--- "II) se -1<=x<2 --> -2x+4-x-1+3x >= 0 --> x >= 0 --> absurdo --> S"={} interseção [-1,2] --> S"'={}"

         - Cuidado com os cálculos: -2x+4-x-1+3x>=0 --> 3>=0 . Perceba que o resultado final da inequação fica independente de x, e é ainda uma verdade, pois 3 é sempre maior ou igual a 0, logo a intersecção da condição de existência para se extrair o módulo e o resultado final, que é todos os valores reais possíveis de x, é a própria condição de existência para se extrair o módulo.

3---   "S = S' U S" U S"' = [-5/2,-1) U {} U [2,+inf) --> S = [-5/2,-1) U [2,+inf) --> E porque deve ser união aqui?"
     
        - A união deve ocorrer pois S' , S" e S'" são informações independentes, ou seja, não vão interferir uma nas outras, pois estamos dizendo no começo de cada procedimento qual deverá a condição de x para que possamos extrair o módulo de cada parcela de certa forma. E como desejamos saber qual é o conjunto solução com todas as possíveis possibilidades, unimos elas em uma só.

         Obs1: em relação a "2", caso o resultado final fosse independente de x e uma informação falsa, o conjunto solução dele seria vazio, ou seja, não há um valor de x que satisfaça a condição.
         Obs2: Não consegui chegar no resultado do gabarito, peço que confira ele novamente, por favor.

Abraços, bons estudos, se tiver mais dúvidas terei prazer em responder, se souber é claro rsrrs.

FreddieMercury escreveu:Cheguei neste resultado:



Responderei as suas dúvidas em ordem :

1--- "I) se x<-1 --> -2x+4+x+1+3x >= 0 --> x >= -5/2 --> S'=(-inf,-1[ interseção [-5/2,+inf) --> S'=[-5/2,-1) --> Obs.: Porque deve ser interseção aqui?"
     
         - Deve-se utilizar a intersecção neste caso, pois estamos dizendo que x é necessariamente menor que -1, assim é uma condição de existência para que possamos extrair o módulo nas condições propostas anteriormente, como  por exemplo, extrair o módulo de x+1 na forma -x-1, chegando no resultado final como x sendo maior ou igual a -5/2. Logo, deve-se buscar a intersecção entre elas, pois desejamos que as duas ocorram ao mesmo tempo.

2--- "II) se -1<=x<2 --> -2x+4-x-1+3x >= 0 --> x >= 0 --> absurdo --> S"={} interseção [-1,2] --> S"'={}"

         - Cuidado com os cálculos: -2x+4-x-1+3x>=0 --> 3>=0 . Perceba que o resultado final da inequação fica independente de x, e é ainda uma verdade, pois 3 é sempre maior ou igual a 0, logo a intersecção da condição de existência para se extrair o módulo e o resultado final, que é todos os valores reais possíveis de x, é a própria condição de existência para se extrair o módulo.

3---   "S = S' U S" U S"' = [-5/2,-1) U {} U [2,+inf) --> S = [-5/2,-1) U [2,+inf) --> E porque deve ser união aqui?"
     
        - A união deve ocorrer pois S' , S" e S'" são informações independentes, ou seja, não vão interferir uma nas outras, pois estamos dizendo no começo de cada procedimento qual deverá a condição de x para que possamos extrair o módulo de cada parcela de certa forma. E como desejamos saber qual é o conjunto solução com todas as possíveis possibilidades, unimos elas em uma só.

         Obs1: em relação a "2", caso o resultado final fosse independente de x e uma informação falsa, o conjunto solução dele seria vazio, ou seja, não há um valor de x que satisfaça a condição.
         Obs2: Não consegui chegar no resultado do gabarito, peço que confira ele novamente, por favor.

Abraços, bons estudos, se tiver mais dúvidas terei prazer em responder, se souber é claro rsrrs.

Adorei suas respostas! Bem completass e explicativas. Muito obrigada mesmo, me ajudou bastante!!

Refiz a questão e cheguei no mesmo resultado que o seu, pode ser que o gabarito esteja errado, já que outras respostas dele estavam...