Inequação Modular

por **abelardo** Seg 11 Jul 2011, 12:54

A solução de $x\left | x \right |>x$ é:

R/ $S=\left \{ x \in \mathbb{R}/-1<x<0 \cup x>1 \right \}$

O que fiz:
$\left\{\begin{matrix} x^2>x\\ x^2<-x \end{matrix}\right.$ $\left\{\begin{matrix} x^2-x>0\\ x^2+x<0 \end{matrix}\right.$

Fazendo o estudo dos sinais das inequações, terei como solução para primeira: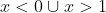 $x<0 \cup x>1$ ; para a segunda $-1<x<0$ . Fazendo a união das soluções não bate com o gabarito... onde errei?

por Diogo Seg 11 Jul 2011, 21:20

1) Na condição de que x > 0, temos:

x² > x

x² - x > 0 ----> x < 0 ou x >1

Portanto, levando em conta a condição, temos que:

x > 1 (I)

2) Na condição de que x < 0, temos:

- x² > x

x² + x < 0 ----> -1 < x < 0

Dessa forma:

-1 < x < 0 (II)

Fazendo a união entre (I) e (II), encontramos:

S = { x Ε R / -1 < x < 0 U x > 1}

por **abelardo** Ter 12 Jul 2011, 12:00

Obrigado Diogo, agora vi o meu erro. Eu deveria só inverter o sinal de x (o do módulo) no segundo caso e não mexer na desigualdade e nem nos sinais dos outros.

por Conteúdo patrocinado

Inequação Modular

Inequação Modular

Re: Inequação Modular

Re: Inequação Modular

Re: Inequação Modular

Um fórum livre e democrático.