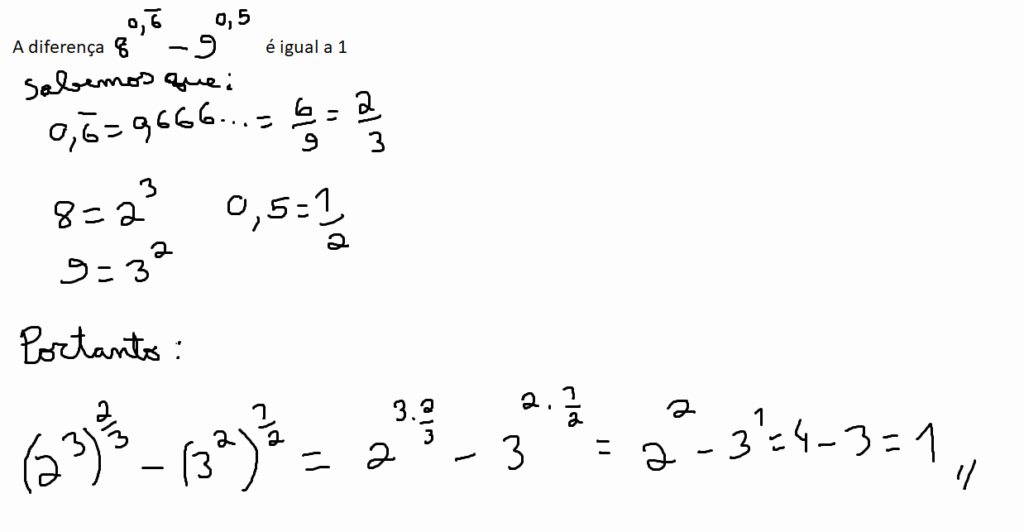EPCAR 2005
3 participantes
Página 1 de 1
 EPCAR 2005
EPCAR 2005
Analise as afirmativas seguintes e classifique-as em (V) verdadeiras ou (F) falsas.
( ) Soma-se um número n ao numerador e ao denominador da fração [latex]\dfrac{3}{2}[/latex] e ela tem um aumento de 20%. Então n é igual a 3.
( ) A diferença [latex]8^{0,\overline{6}}-9^{0,5}[/latex] é igual a 1.
( ) O menor número natural n, diferente de zero, que torna o produto de 3888 por n um cubo perfeito é 12.
A sequência correta para essa classificação é:
a) F, V, F
b) F, V, V
c) V. F, V.
d) V, V, V.
( ) Soma-se um número n ao numerador e ao denominador da fração [latex]\dfrac{3}{2}[/latex] e ela tem um aumento de 20%. Então n é igual a 3.
( ) A diferença [latex]8^{0,\overline{6}}-9^{0,5}[/latex] é igual a 1.
( ) O menor número natural n, diferente de zero, que torna o produto de 3888 por n um cubo perfeito é 12.
A sequência correta para essa classificação é:
a) F, V, F
b) F, V, V
c) V. F, V.
d) V, V, V.
Última edição por lana_bra101 em Qui 20 maio 2021, 00:31, editado 1 vez(es)
lana_bra101- Iniciante
- Mensagens : 10
Data de inscrição : 19/04/2021
Localização : RJ

GBRezende- Jedi

- Mensagens : 227
Data de inscrição : 18/10/2017
Idade : 27
Localização : Rio de Janeiro, RJ, Brasil
lana_bra101 gosta desta mensagem
 Re: EPCAR 2005
Re: EPCAR 2005
Analise as afirmativas seguintes e classifique-as em (V) verdadeiras ou (F) falsas.
(F) Soma-se um número n ao numerador e ao denominador da fração 3/2 e ela tem um aumento de 20%. Então n é igual a 3.
Se a fração é imprópria -- como é o caso desta (numerador maior que o denominador), onde o resultado é um número maior do que 1 -- e aumentamos numerador e denominador de quantidades iguais, a diferença relativa entre ambos diminui, a quantidade do numerador fica mais próxima da do denominador e a fração tende para 1. Portanto a fração resulta um número menor; ou seja, há redução e não aumento.
Se a fração é própria -- numerador menor que o denominador, resultando num número menor do que 1 -- ao aumentar de quantidades iguais o numerador e o denominador a fração também tende para 1, pois a diferença relativa entre ambos diminui, porém como a fração era menor do que 1 quanto mais ela tender a 1 mais ela aumenta. Portanto neste caso há aumento.
Veja dois exemplos:
[latex]\\\frac{3}{2}= 1,5 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{3+8}{2+8}=\frac{11}{10}=1,1 \\\\ \frac{2}{3}=0,66 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{2+7}{3+7}=\frac{9}{10}=0,9[/latex]
(V) A diferença [latex]8^{0,\bar{6}}-9^{0,5}[/latex] é igual a 1.
[latex]0,\bar{6} = \frac{2}{3}[/latex] e 8 = 2³
[latex]8^{0,\bar{6}}-9^{0,5} = \left(2^{3} \right )^{\frac{2}{3}}-\left(3^{2} \right )^{\frac{1}{2}} = 2^\frac{6}{3}- 3^\frac{2}{2} = 2^{2}-3 = 1[/latex]
(V) O menor número natural n, diferente de zero, que torna o produto de 3888 por n um cubo perfeito é 12.
3 888 = 24.35
o cubo superior mais próximo é 26.36 e para chegar nele precisamos multiplicar o 3 888 por 22.31 = 4.3 = 12
(F) Soma-se um número n ao numerador e ao denominador da fração 3/2 e ela tem um aumento de 20%. Então n é igual a 3.
Se a fração é imprópria -- como é o caso desta (numerador maior que o denominador), onde o resultado é um número maior do que 1 -- e aumentamos numerador e denominador de quantidades iguais, a diferença relativa entre ambos diminui, a quantidade do numerador fica mais próxima da do denominador e a fração tende para 1. Portanto a fração resulta um número menor; ou seja, há redução e não aumento.
Se a fração é própria -- numerador menor que o denominador, resultando num número menor do que 1 -- ao aumentar de quantidades iguais o numerador e o denominador a fração também tende para 1, pois a diferença relativa entre ambos diminui, porém como a fração era menor do que 1 quanto mais ela tender a 1 mais ela aumenta. Portanto neste caso há aumento.
Veja dois exemplos:
[latex]\\\frac{3}{2}= 1,5 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{3+8}{2+8}=\frac{11}{10}=1,1 \\\\ \frac{2}{3}=0,66 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{2+7}{3+7}=\frac{9}{10}=0,9[/latex]
(V) A diferença [latex]8^{0,\bar{6}}-9^{0,5}[/latex] é igual a 1.
[latex]0,\bar{6} = \frac{2}{3}[/latex] e 8 = 2³
[latex]8^{0,\bar{6}}-9^{0,5} = \left(2^{3} \right )^{\frac{2}{3}}-\left(3^{2} \right )^{\frac{1}{2}} = 2^\frac{6}{3}- 3^\frac{2}{2} = 2^{2}-3 = 1[/latex]
(V) O menor número natural n, diferente de zero, que torna o produto de 3888 por n um cubo perfeito é 12.
3 888 = 24.35
o cubo superior mais próximo é 26.36 e para chegar nele precisamos multiplicar o 3 888 por 22.31 = 4.3 = 12

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
GBRezende e lana_bra101 gostam desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» EPCAR 3A - 2005
» epcar 2005 - álgebra
» [EPCAr 2005] - Divisibilidade
» EPCAr 2005 - Geometria
» EPCAr 2005 - Geometria
» epcar 2005 - álgebra
» [EPCAr 2005] - Divisibilidade
» EPCAr 2005 - Geometria
» EPCAr 2005 - Geometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos