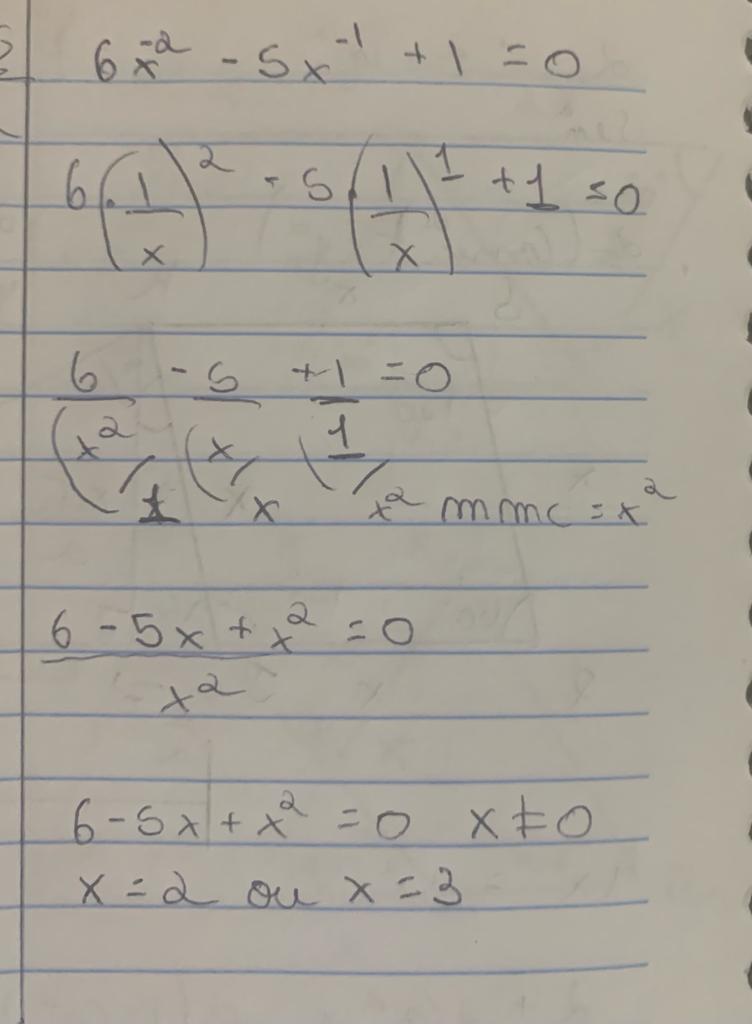Equações :primeiro e segundo grau
3 participantes
Página 1 de 1
 Equações :primeiro e segundo grau
Equações :primeiro e segundo grau
Resolva a equação:6x^-2-5x^-1+1=0
Iasmim1234- Iniciante
- Mensagens : 8
Data de inscrição : 21/04/2021
 Re: Equações :primeiro e segundo grau
Re: Equações :primeiro e segundo grau
[latex] A^{-1} = \frac{1}{A}^{1} ,\ \ \ \ \ logo\ ficaria\ : \\\ 6.\frac{1}{x^{2}} - 5.\frac{1}{x} + 1 =0 \ \\\ \\\ \\\ \\\ mmc(x^{2},x,1) =x^{2} \\\ \\\ \\\ \\\ 6 - 5x + x^{2} = 0 \\\ \\\ \\\ raizes\ 2\ e\3[/latex]
____________________________________________
''I have nothing to offer but blood, toil, tears and sweat''
Sir Winston Churchill

MarioCastro- Elite Jedi

- Mensagens : 274
Data de inscrição : 20/04/2019
Idade : 21
Localização : Rio de Janeiro, RJ
 Re: Equações :primeiro e segundo grau
Re: Equações :primeiro e segundo grau
Eu n entendi,poderia me explicar passo a passo,pfvr ?
Iasmim1234- Iniciante
- Mensagens : 8
Data de inscrição : 21/04/2021
 Re: Equações :primeiro e segundo grau
Re: Equações :primeiro e segundo grau
____________________________________________
''I have nothing to offer but blood, toil, tears and sweat''
Sir Winston Churchill

MarioCastro- Elite Jedi

- Mensagens : 274
Data de inscrição : 20/04/2019
Idade : 21
Localização : Rio de Janeiro, RJ
 Re: Equações :primeiro e segundo grau
Re: Equações :primeiro e segundo grau
Eu n entendi a parte do mmc ,eu dividi todos eles por x e o meu 6/x^2 deu 6x.
Iasmim1234- Iniciante
- Mensagens : 8
Data de inscrição : 21/04/2021
 Re: Equações :primeiro e segundo grau
Re: Equações :primeiro e segundo grau
O mmc entre um número e o múltiplo dele sempre será o próprio multiplo.
mmc( 5, 25 ) = 25
qual o menor múltiplo comum positivo entre eles ? (mmc)
multiplos de 5 : {0,5,10,15,20,25,30...}
multiplos de 25 : {0,25,50....} logo mmc entre 5 e 5^2 é o proprio 5^2
multiplos de x : {0, x, 2x, 3x, 4x,....., (x-2)x, (x-1)x, x.x, ......}
multiplos de x^2 :{0, x^2, 2x^2, 3x^2, ....}
o mmc entre (x, x^2 ) = x^2
Uma maneira de fazer fugindo do mmc seria multiplicar a equaçao inteira por "x"
x(6/x^2) - x(5/x) + x(1) = x(0)
6/x - 5 + x = 0
do mesmo jeito teria fazer mmc, agora entre x e 1, o que é mais fácil.
Ou multiplicar a equaçao inteira por x de novo.
Multiplicar tudo por um número do denominador sempre é uma saída, mas será mais trabalhosa
mmc( 5, 25 ) = 25
qual o menor múltiplo comum positivo entre eles ? (mmc)
multiplos de 5 : {0,5,10,15,20,25,30...}
multiplos de 25 : {0,25,50....} logo mmc entre 5 e 5^2 é o proprio 5^2
multiplos de x : {0, x, 2x, 3x, 4x,....., (x-2)x, (x-1)x, x.x, ......}
multiplos de x^2 :{0, x^2, 2x^2, 3x^2, ....}
o mmc entre (x, x^2 ) = x^2
Uma maneira de fazer fugindo do mmc seria multiplicar a equaçao inteira por "x"
x(6/x^2) - x(5/x) + x(1) = x(0)
6/x - 5 + x = 0
do mesmo jeito teria fazer mmc, agora entre x e 1, o que é mais fácil.
Ou multiplicar a equaçao inteira por x de novo.
Multiplicar tudo por um número do denominador sempre é uma saída, mas será mais trabalhosa
____________________________________________
''I have nothing to offer but blood, toil, tears and sweat''
Sir Winston Churchill

MarioCastro- Elite Jedi

- Mensagens : 274
Data de inscrição : 20/04/2019
Idade : 21
Localização : Rio de Janeiro, RJ
 Re: Equações :primeiro e segundo grau
Re: Equações :primeiro e segundo grau
6 .... 5
--- - --- + 1 = 0 ---> multiplicando tudo por x² --->
x² ... x
6 - 5.x + x² = 0
x² - 5.x + 6 = 0 ---> x' = 2 e x" = 3
--- - --- + 1 = 0 ---> multiplicando tudo por x² --->
x² ... x
6 - 5.x + x² = 0
x² - 5.x + 6 = 0 ---> x' = 2 e x" = 3

Elcioschin- Grande Mestre

- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Tópicos semelhantes
Tópicos semelhantes» funcao do primeiro grau e segundo grau
» Equação do primeiro e do segundo grau
» EQUAÇÃO DO PRIMEIRO E SEGUNDO GRAU
» Equação primeiro e segundo grau
» FUNÇÃO DO PRIMEIRO E SEGUNDO GRAU
» Equação do primeiro e do segundo grau
» EQUAÇÃO DO PRIMEIRO E SEGUNDO GRAU
» Equação primeiro e segundo grau
» FUNÇÃO DO PRIMEIRO E SEGUNDO GRAU
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos