Geometria

Sejam O e H o circuncentro e ortocentro de um triângulo agudo ABC, respectivamente, como na figura abaixo. Mostre que ∠BAH = ∠CAO.

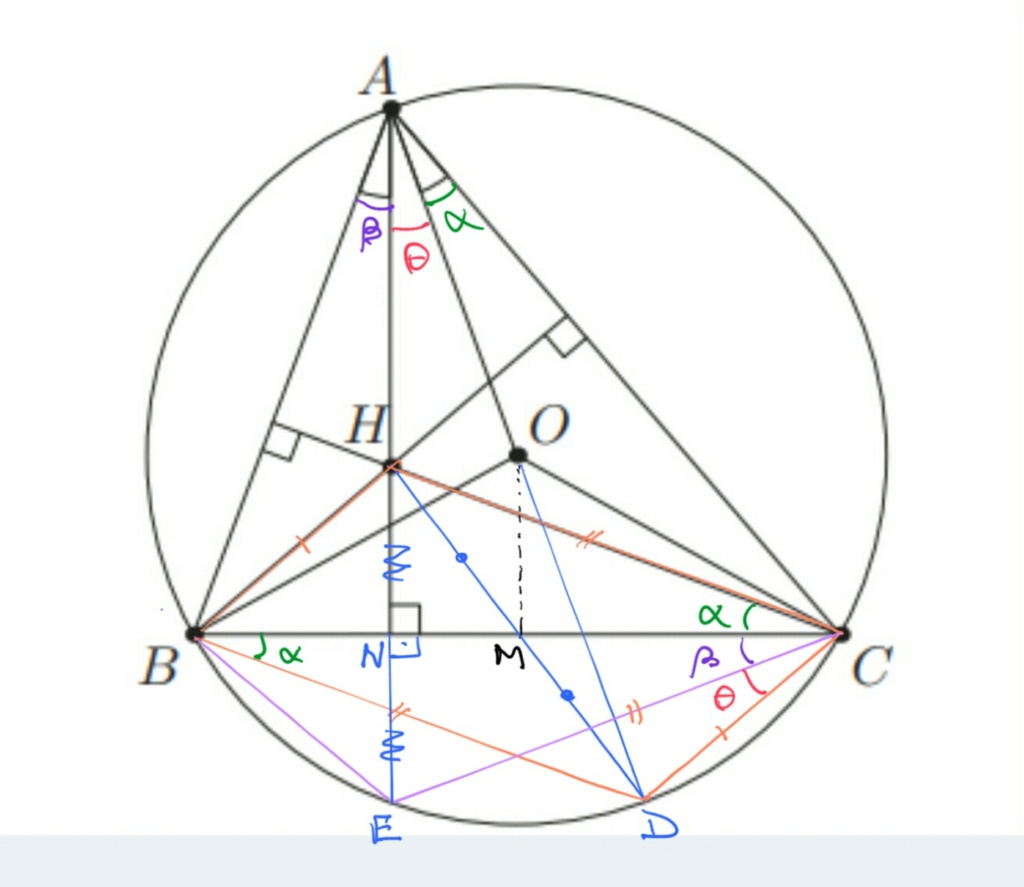
____________________________ sinceramente não sei porquê esta figura ficou gigante, fiz igual de outras vezes

terminologia adotada
[latex]\\\alpha = \angle CAO \\ \beta = \angle BAH \\ \theta = \angle OAH[/latex]

Seja M a projeção de O sobre o lado BC, então M é ponto médio de BC.
O segmento que passa por H e M encontra a circunferência em D. Por uma propriedade do ortocentro HM = MD. Desta forma MD e BC são as diagonais do paralelogramo BHCD.
Mote que os ângulos inscritos [latex]\alpha[/latex] em A e B vêem o mesmo arco CD, portanto o prolongamento AO também encontra a circunferência em D.
O prolongamento da altura em relação ao lado BC encontra a circunferência em E. Novamente por uma propriedade do ortocentro HN = NE e os ângulos inscritos assinalados como [latex]\beta[/latex] em A e C vêem o mesmo arco BE.
No paralelogramo BHCD anotamos o outro ângulo [latex]\alpha[/latex] alterno interno junto ao vérticde C.

No [latex]\Delta CHE[/latex], CN é altura e HN = NE portanto o triângulo é isósceles e consequentemente CH = CE. Portanto os ângulos do vértice definidos pela altura são iguais ----->  [latex]\alpha = \beta[/latex]


corolário: para o triângulo ABC
- AO e AH são isogonais do vértice A
e analogamente
- BO e BH são isogonais do vértice B
- CO e CH são isogonais do vértice C

outro modo, muito mais fácil.