Hipérbole
4 participantes
Página 1 de 1
Hipérbole
por L. José Ter 12 Jan 2021, 20:13
Considere uma elipse e uma hipérbole no plano cartesiano, ambas com centro na origem e eixos de simetria coincidindo com os eixos coordenados.
Sabendo que os pontos (3, 0) e (√(15/2), 1) pertencem à elipse e que (√2, 0) e (2, 1) pertencem à hipérbole, determine os pontos de interseção dessas cônicas.
Gabarito: (-√6,-√2), (-√6, √2), (√6, -√2) e (√6, √2)
Sabendo que os pontos (3, 0) e (√(15/2), 1) pertencem à elipse e que (√2, 0) e (2, 1) pertencem à hipérbole, determine os pontos de interseção dessas cônicas.
Gabarito: (-√6,-√2), (-√6, √2), (√6, -√2) e (√6, √2)
L. José- Jedi
- Mensagens : 219
Data de inscrição : 09/07/2018
Idade : 25
Localização : Recife, Pernambuco, Brasil
Re: Hipérbole
por Elcioschin Ter 12 Jan 2021, 21:47
Elipse
x²/A² + y²/B² = 1
(3, 0) ---> 3²/A² + 0²/B² = 1 ---> Calcule A
(√(15/2), 1) ---> (15/2)/A² + 0²/B² = 1 ---> Calcule B
Hipérbole: x²/a² - y²/b² = 1
(√2, 0) --> Calcule a
(2, 1) ---> Calcule b
Monte as equações das duas curvas
Resolva o sistema e encontre os 4 pontos de encontro
x²/A² + y²/B² = 1
(3, 0) ---> 3²/A² + 0²/B² = 1 ---> Calcule A
(√(15/2), 1) ---> (15/2)/A² + 0²/B² = 1 ---> Calcule B
Hipérbole: x²/a² - y²/b² = 1
(√2, 0) --> Calcule a
(2, 1) ---> Calcule b
Monte as equações das duas curvas
Resolva o sistema e encontre os 4 pontos de encontro
Elcioschin- Grande Mestre
- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Cônicas
por DGL72021 Qui 29 Dez 2022, 20:11
(9/a²)+(0/b²)=1----->a=3
(15/18)+(1/b²)=1----->1/b² = 3/18---->b²=6
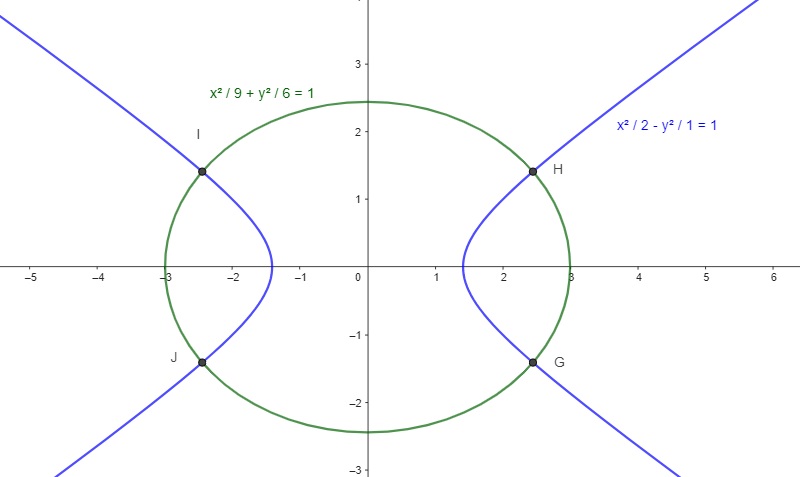
(x²/9)+(y²/6)=1 equação reduzida elipse
2/a²=1--->a²=2
(4/2)+(1/b²)=1---->b²=-1
(x²/2)+y²=1 equação reduzida hipérbole.
Mestre não sei prosseguir daí, eu faço o sistema e não encontro os valores do gabarito.
(15/18)+(1/b²)=1----->1/b² = 3/18---->b²=6
(x²/9)+(y²/6)=1 equação reduzida elipse
2/a²=1--->a²=2
(4/2)+(1/b²)=1---->b²=-1
(x²/2)+y²=1 equação reduzida hipérbole.
Mestre não sei prosseguir daí, eu faço o sistema e não encontro os valores do gabarito.
DGL72021- Jedi
- Mensagens : 209
Data de inscrição : 11/02/2021
Re: Hipérbole
por Elcioschin Qui 29 Dez 2022, 22:26
Você errou na equação da hipérbole (erro de sinal). Corrija
Complete a sua solução e mostre os valores a que vc chegou.
Complete a sua solução e mostre os valores a que vc chegou.
Elcioschin- Grande Mestre
- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
DGL72021 gosta desta mensagem
Re: Hipérbole
por petras Qui 29 Dez 2022, 22:43
Imagem para ajudar
____________________________________________
_______________________________
"Ex nihilo nihil fit"
petras- Monitor
- Mensagens : 2117
Data de inscrição : 10/06/2016
Idade : 59
Localização : bragança, sp, brasil
DGL72021 gosta desta mensagem
hipérbole
por DGL72021 Sex 30 Dez 2022, 16:38
(9/a²)+(0/b²)=1---->a=3
(15/18)+(1/b²)=1--->1/b² = 3/18---->b²=6
(2/a²)+(0/b²)=1---->a²=2
(4/2)-(1/b²)=1----->b²=1
(x²/9)+(y²/6)=1 .6----->(2x²/3)+y²=6
(x²/2)-y²=1
(x²/2)+(2x²/3)=7 somei as duas equações logo o y²-y²=0
(4x²+3x²)/6=7----x²=6
substituindo na equação vem:
(6/2)-y²=1----->y²=2
logo:(√6,√2);(-√6,√2);(√6,-√2);(-√6,-√2)
(15/18)+(1/b²)=1--->1/b² = 3/18---->b²=6
(2/a²)+(0/b²)=1---->a²=2
(4/2)-(1/b²)=1----->b²=1
(x²/9)+(y²/6)=1 .6----->(2x²/3)+y²=6
(x²/2)-y²=1
(x²/2)+(2x²/3)=7 somei as duas equações logo o y²-y²=0
(4x²+3x²)/6=7----x²=6
substituindo na equação vem:
(6/2)-y²=1----->y²=2
logo:(√6,√2);(-√6,√2);(√6,-√2);(-√6,-√2)
DGL72021- Jedi
- Mensagens : 209
Data de inscrição : 11/02/2021
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
