Tipos de Funções: injetora, bijetora, sobrejetora

Sejam f e g duas funções cujos domínio e contradomínio são o conjunto dos números reais. Considere as afirmações a seguir: 
I. Sempre que g é injetora, g o f: R → R é injetora. 
II. Se f é decrescente e g também é decrescente, então, f o g também é decrescente. 
III. Se f é crescente, g é decrescente e g(x) > 0 para todo x real, então, f/g é crescente. 
IV. Se f é decrescente e g é decrescente, então, f + g é decrescente. 
V. Se os gráficos de f e g não interceptam o eixo das abscissas, então, o gráfico de f ∙ g também não intercepta o eixo das abscissas.

A quantidade de afirmações INCORRETAS é: 
a) 1 
b) 2 
c) 3 
d) 4

Gab.: B

Para fazer questão de compostas, recomendo o uso de um esqueminha como esse:

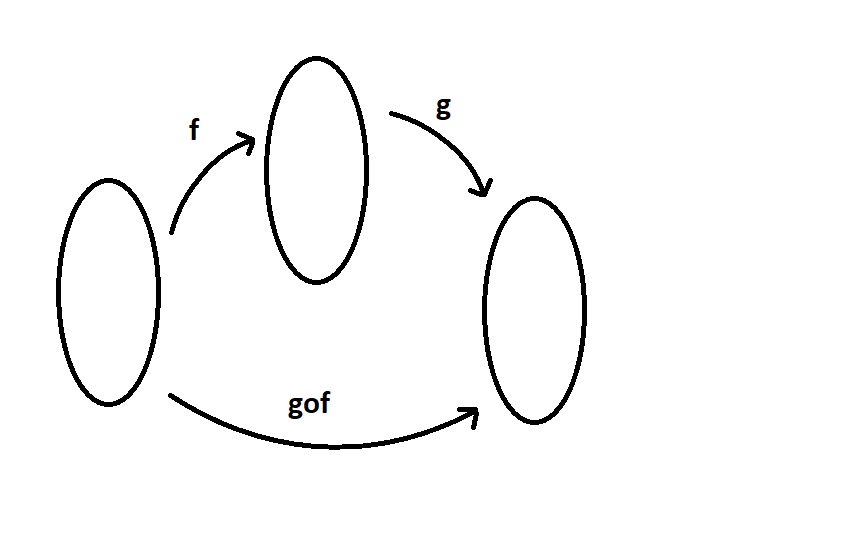
I - Falsa. Mesmo que g seja injetora, caso f não seja, a função composta não será injetora.

II - Verdadeiro.
f(x1)>f(x2), x1>x2
g(x'1)>g(x'2), x'1>x'2

para f(x1) = x'1 e f(x2) = x'2:
g(f(x1))>g(f(x2)), x1>x2
comprovado gof é descrescente.

III - Falso. Supondo que, para dado intervalo, f é negativo e cresce pouco, e g decresce rapidamente, f/g vai resultar em um número negativo de módulo cada vez maior, ou seja, será decrescente.

IV - Verdadeiro. Se as duas parcelas decrescem, a soma decresce.

V - Verdadeiro. Interceptar o eixo das abcissas significa mudar de sinal. Se nenhum dos fatores sofre alteração no sinal, o produto também não sofrerá.

Espero ter ajudado!

Ajudou demais, muito obrigado!