Maximizar corda

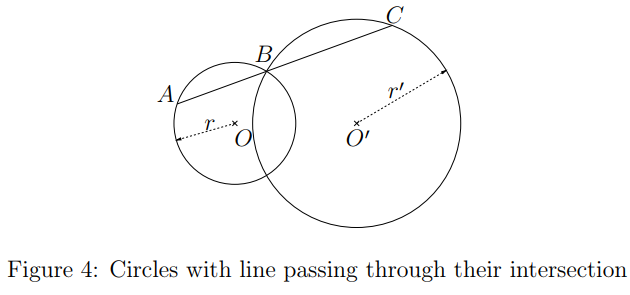
In Figure 4, the chords AB and BC are aligned. Mark the characteristic that would make
the length of AC maximum:
(a) The extremum point A must be aligned to OO′
(b) AB must be equal to BC
(c) AB/r = BC/r′
(d) AC must be paralell to OO′
(e) None of the above characteristics would maximize AC

Ainda não encontrei uma maneira de provar matematicamente que a resposta é (d), embora pareça um tanto intuitivo...

Olá Ashitaka!


Traçando EF paralelo a OO', formamos 2 quadriláteros inscritos AEBD e BCFD. Com isso ∠BAD = ∠DEB e ∠ACD = ∠DFE, e consequentemente os triângulos ADC e EDF são semelhantes. Portanto, para maximizarmos o lado AC, basta maximizarmos também AD e CD, que são cordas das circunferências.  Ora, as cordas são maximizadas quando passam pelo centro da circunferência de modo a ter comprimento igual ao diâmetro. Isso irá ocorrer quando A = E e C = F, de modo que EF de fato representa o caso de máximo do comprimento de AC.

Victor011 escreveu:[...] Portanto, para maximizarmos o lado AC, basta maximizarmos também AD e CD, que são cordas das circunferências. 

Olá, Victor! Obrigado pela resposta.
Fiquei um pouco desconfortável com essa afirmação que destaquei porque ela não me parece óbvia.

Mas sua resolução me levou a outro raciocínio que me deixou satisfeito.
Ignorar os quadriláteros e olhar apenas para os triângulos EDF e ADC é uma boa alternativa. Se eles são semelhantes, significa que um é uma ampliação do outro. Qual será maior? O que tem os maiores lados. Quem tem o maior lado é o que tem a maior corda, e a maior corda é o diâmetro da circunferência. Isso mata a questão.

Ashitaka, eu só falei dos quadriláteros inscritos para facilitar a visualização dos ângulos que eu marquei como iguais, mas podemos de fato ignorar os quadriláteros.
Em relação à afirmação que eu fiz, ela é praticamente o que você explicou kkkkkk a única "diferença" é que você comparou EDF com ADC e eu analisei somente ADC, com AC podendo variar em torno de B. Sendo assim, dizer que AC é maximizado quando os lados AD e CD do triângulo também forem, é o mesmo que dizer que estamos em busca do maior triângulo semelhante ADC (conforme AC varia), que é aquele que tem os maiores lados (AD e CD), como você disse. 
De qualquer forma, o seu raciocínio está corretíssimo

Victor011 escreveu:Ashitaka, eu só falei dos quadriláteros inscritos para facilitar a visualização dos ângulos que eu marquei como iguais, mas podemos de fato ignorar os quadriláteros.
Em relação à afirmação que eu fiz, ela é praticamente o que você explicou kkkkkk a única "diferença" é que você comparou EDF com ADC e eu analisei somente ADC, com AC podendo variar em torno de B. Sendo assim, dizer que AC é maximizado quando os lados AD e CD do triângulo também forem, é o mesmo que dizer que estamos em busca do maior triângulo semelhante ADC (conforme AC varia), que é aquele que tem os maiores lados (AD e CD), como você disse. 
De qualquer forma, o seu raciocínio está corretíssimo

Sim, é verdade, é que, do jeito que está escrito, eu não fiz o elo com a semelhança de triângulos (aí a importância de saber a hora de parar hahaha). Mas, de fato, fazendo, acaba dando um raciocínio análogo ao que eu fiz. Novamente, agradeço pela contribuição. E legal essa foto do Itachi aí.