Geometria espacial - comprimento de cordas
2 participantes
Página 1 de 1
 Geometria espacial - comprimento de cordas
Geometria espacial - comprimento de cordas
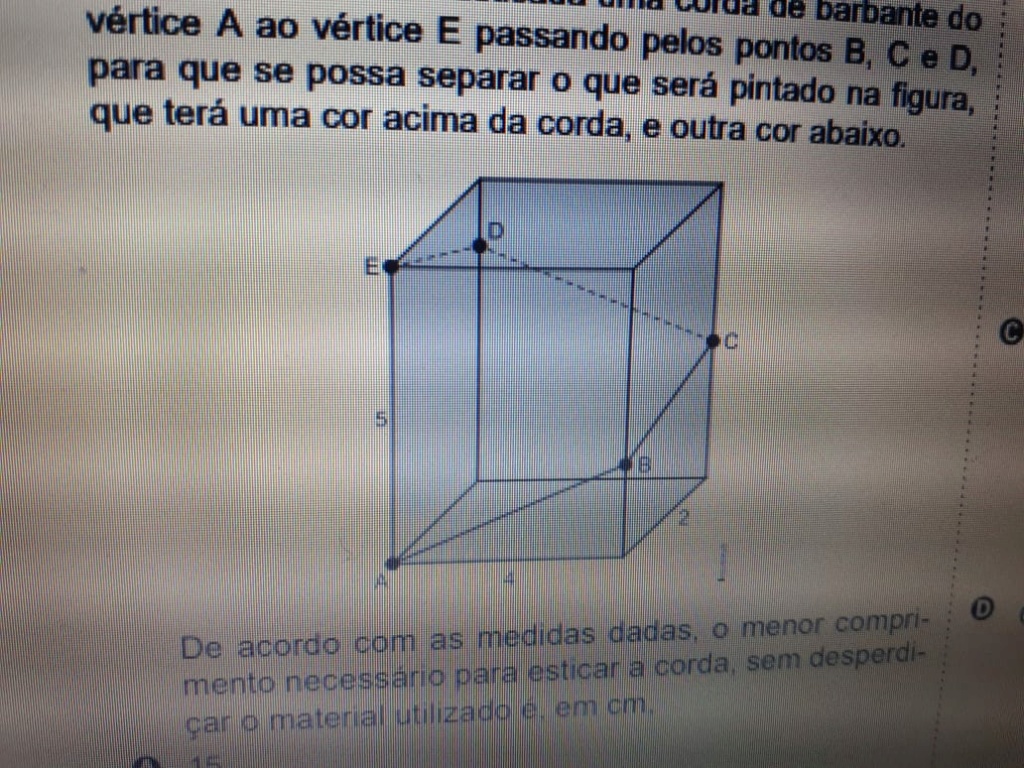
Em volta do paralelepípedo reto-retângulo mostrado
na figura abaixo será esticada uma corda de barbante do
vértice A ao vértice E passando pelos pontos B, C e D,
para que se possa separar o que será pintado na figura,
que terá uma cor acima da corda, e outra cor abaixo.
De acordo com as medidas dadas, o menor compri-
mento necessário para esticar a corda, sem desperdi-
çar o material utilizado é, em cm,
A 15
B 13
C 16
D 14
E 17
Não tenho o gabarito. Não consegui pegar o caminho pra resolver a questão. Alguém pode me ajudar?
na figura abaixo será esticada uma corda de barbante do
vértice A ao vértice E passando pelos pontos B, C e D,
para que se possa separar o que será pintado na figura,
que terá uma cor acima da corda, e outra cor abaixo.
De acordo com as medidas dadas, o menor compri-
mento necessário para esticar a corda, sem desperdi-
çar o material utilizado é, em cm,
A 15
B 13
C 16
D 14
E 17
Não tenho o gabarito. Não consegui pegar o caminho pra resolver a questão. Alguém pode me ajudar?

Enzo _Sergi- Recebeu o sabre de luz

- Mensagens : 102
Data de inscrição : 30/07/2020
Idade : 21
Localização : Porto Alegre, RS, Brasil
 Re: Geometria espacial - comprimento de cordas
Re: Geometria espacial - comprimento de cordas
Minha opinião:
Ver figura abaixo. Existem simetrias na figura.
1) O ponto C deve estar no meio da aresta NG: NC = GC = 5/2
2) Seja MB = x ---> HD = x
No ∆ retângulo AMB ---> AB = √(x² + 16)
No ∆ retângulo BKC ---> BC = √[(5/2 - x)² + 4]
No ∆ retângulo DLC ---> CD = √[(5/2 - x)² + 16]
No ∆ retângulo DHE ---> DE = √(x² + 4)
Seja y o comprimento total da corda ---> y = AB + BC + CD + DE --->
y = √(x² + 16) + √[(5/2 - x)² + 4] + √[(5/2 - x)² + 16] + √(x² + 16)
O caminho é calcular a derivada y' , igualá-la a zero e calcular x
É trabalhoso!
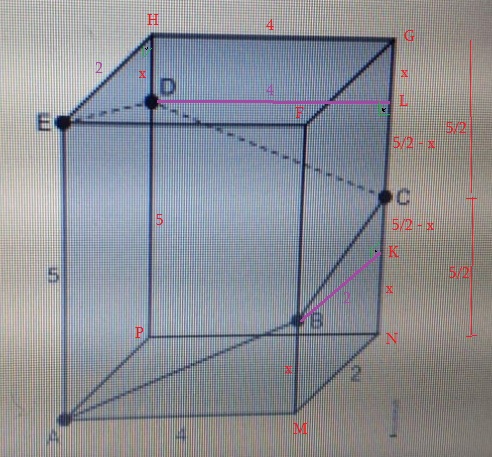
Ver figura abaixo. Existem simetrias na figura.
1) O ponto C deve estar no meio da aresta NG: NC = GC = 5/2
2) Seja MB = x ---> HD = x
No ∆ retângulo AMB ---> AB = √(x² + 16)
No ∆ retângulo BKC ---> BC = √[(5/2 - x)² + 4]
No ∆ retângulo DLC ---> CD = √[(5/2 - x)² + 16]
No ∆ retângulo DHE ---> DE = √(x² + 4)
Seja y o comprimento total da corda ---> y = AB + BC + CD + DE --->
y = √(x² + 16) + √[(5/2 - x)² + 4] + √[(5/2 - x)² + 16] + √(x² + 16)
O caminho é calcular a derivada y' , igualá-la a zero e calcular x
É trabalhoso!


Elcioschin- Grande Mestre

- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Geometria espacial - comprimento de cordas
Re: Geometria espacial - comprimento de cordas
Obrigado Elcioschin!
Mas eu estou no ensino médio ainda, não sei se essa questão é pra mim hehehe
Mas eu estou no ensino médio ainda, não sei se essa questão é pra mim hehehe
Enzo _Sergi- Recebeu o sabre de luz

- Mensagens : 102
Data de inscrição : 30/07/2020
Idade : 21
Localização : Porto Alegre, RS, Brasil
 Re: Geometria espacial - comprimento de cordas
Re: Geometria espacial - comprimento de cordas
Uma sugestão para calcular sem derivadas. Vai ser uma "diversão" para você!
Planifique o paralelepípedo, em escala, colocando as suas seis faces num único plano.
Note que existem várias maneiras de fazer isto. Você pode girar uma face em torno de um dos vértices e colocar esta face junto de uma nova face.
Faça isto, até que você consiga traçar o segmento de reta AB passando por todas as 6 faces.
Agora é só aplicar Pitágoras e calcular AB.
Obs.: não desenhei as faces AMNP e e EFGH porque elas não fazem parte do percurso
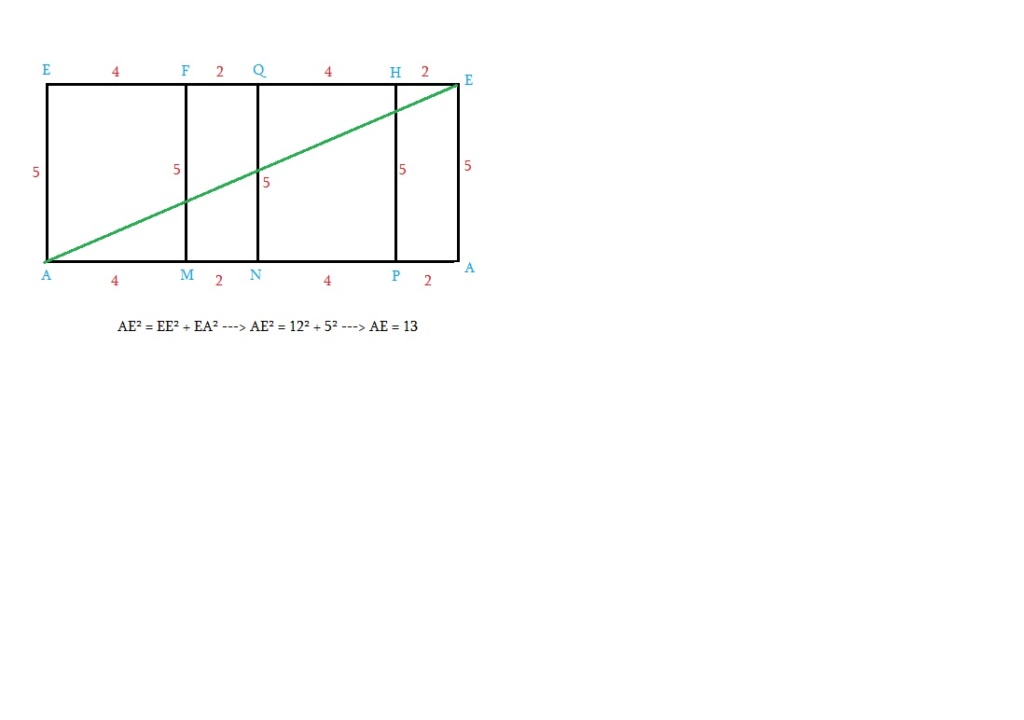
Planifique o paralelepípedo, em escala, colocando as suas seis faces num único plano.
Note que existem várias maneiras de fazer isto. Você pode girar uma face em torno de um dos vértices e colocar esta face junto de uma nova face.
Faça isto, até que você consiga traçar o segmento de reta AB passando por todas as 6 faces.
Agora é só aplicar Pitágoras e calcular AB.
Obs.: não desenhei as faces AMNP e e EFGH porque elas não fazem parte do percurso


Elcioschin- Grande Mestre

- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Tópicos semelhantes
Tópicos semelhantes» Geomatria Espacial - Calcular o menor comprimento
» geometria espacial 3
» Geometria Espacial - UEM
» geometria espacial
» Geometria Espacial
» geometria espacial 3
» Geometria Espacial - UEM
» geometria espacial
» Geometria Espacial
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












