IME lugar geométrico

por Xm280 Sex 25 Set 2020, 10:43

(IME-78) De um ponto P(x,y) traçam-se duas tangentes à elipse x²/16+y²/9 = 1. Determine a equação do lugar geométricodo ponto P, de tal forma que estas tangentes sejam perpendiculares entre si.

Gabarito:

por **SilverBladeII** Qui 14 Jan 2021, 19:01

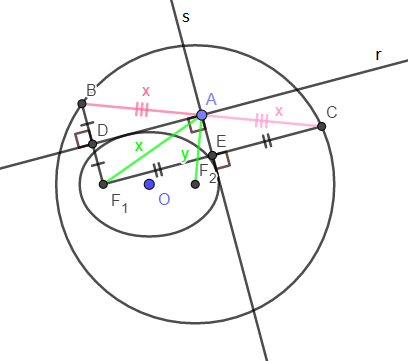
Seja [latex]O[/latex] a origem do plano. Se a elipse tem equação [latex]\frac{x^2}{a^2}+\frac{y^2}{b^2}=1[/latex],
Seja [latex]A=(m, n)[/latex] um ponto satisfazendo as condições do enunciado, [latex]F_1=(-c, 0), F_2=(c, 0)[/latex] são focos, eixo maior [latex]a[/latex] e eixo menor [latex]b[/latex].
Tome o círculo diretor [latex]\Gamma[/latex] centrado em [latex]F_2[/latex] e de raio [latex]2a[/latex]. Se [latex]F_1B[/latex] e [latex]F_1C[/latex] são segmentos perpendiculares às tangentes [latex]r[/latex] e [latex]s[/latex], respectivamente, tais que [latex]B,C\in\Gamma[/latex], sabemos que [latex]\overline{F_1D}=\overline{DB}[/latex] e [latex]\overline{F_1E}=\overline{EC}[/latex] (isso independe da perpendicularidade de [latex]r[/latex] e [latex]s[/latex] e será usado mais adiante), de forma que o quadrilátero [latex]AEF_1D[/latex] é um retângulo e [latex]\angle F_2F_1D[/latex] é reto.
Ora, [latex]r[/latex] é mediatriz de [latex]F_1B[/latex] e [latex]s[/latex] é mediatriz [latex]F_1C[/latex], de modo que [latex]\overline{BA}=\overline{F_1A}=\overline{CA}=x[/latex], e daí [latex]A[/latex] é circuncentro de [latex]BCF_1[/latex]. Mas [latex]BCF_1[/latex] é retângulo, de forma que [latex]A[/latex] é ponto médio da hipotenusa e [latex]A,B,C[/latex] são colineares.
[latex]F_2[/latex] é centro de [latex]\Gamma[/latex] e [latex]BC[/latex] é corda de [latex]\Gamma[/latex] com ponto médio [latex]A[/latex], então [latex]F_2A\perp BC[/latex].
Pelo teorema de Pitágoras em [latex]BAF_2[/latex],
[latex]x^2+y^2=\overline{BF_2}^2=4a^2[/latex].
Dessa forma,
[latex]\begin{align*}x^2&=\overline{F_1A}^2\\&=(m-(-c))^2+n^2\\&=m^2+c^2+2mc+n^2\end{align*}[/latex]
e
[latex]\begin{align*}y^2&=\overline{F_2A}^2\\&=(m-(c))^2+n^2\\&=m^2+c^2-2mn+n^2\end{align*}[/latex],
daí,
[latex]2m^2+2c^2+2n^2=x^2+y^2=4a^2\implies m^2+n^2=a^2+b^2[/latex].

Suponha, agora, que o ponto [latex]A=(m, n)[/latex] é tal que
[latex]m^2+n^2=a^2+b^2=r^2[/latex].
Nas notações de anteriormente, lei dos cossenos nos triângulos [latex]F_1OA[/latex] e [latex]F_2OA[/latex]:
[latex]x^2=r^2+c^2-2rc\cos\alpha[/latex]
[latex]y^2=r^2+c^2+2r\cos\alpha[/latex],

de modo que
[latex]x^2+y^2=2r^2+2c^2=2a^2+2b^2+2c^2=4a^2[/latex].
No triângulo [latex]BF_2A[/latex],
[latex]\overline{BF_2}^2=4a^2=x^2+y^2=\overline{BA}^2+\overline{AF_2}^2[/latex]
e, pela volta do teorema de pitágoras, [latex]\angle BAF_2[/latex] é reto. Analogamente, [latex]\angle F_2AC[/latex] é reto, de forma que [latex]B,A,C[/latex] são colineares.
Como [latex]A[/latex] é circuncentro de [latex]BF_1C[/latex], então esse triângulo é retângulo em [latex]F_1[/latex]. [latex]D[/latex] e [latex]E[/latex] também são retos, de modo que o quadrilátero [latex]DF_1EA[/latex] é retângulo, então [latex]A[/latex] pertence ao lugar geométrico desejado.
Assim, o lugar geométricos dos pontos que satisfazem o enunciado são os pontos da circunfência [latex]x^2+y^2=a^2+b^2[/latex].

Hmmm, depois de fazer a volta eu me liguei que a prova da ida é praticamente a mesma da volta, só que ao contrário. Deve dar pra botar uns "se, e somente se" em alguns lugares e reduzir pela metade, mas não vou fazer isso agora.