Desafio Matemática(9.1.3): Geometria Plana

por Lucius Draco Qua 15 Jul 2020, 12:28

Continuando com a série de desafios!
(Resposta será postada às 22:00h)

(Colégio Naval) Na figura abaixo, o ponto P do menor arco AB dista 6 cm e 10 cm, respectivamente, das tangentes AQ e BQ. A distância, em cm, do ponto P à corda AB é igual a:

Desafio Matemática(9.1.3): Geometria Plana Sem_tz24

a)√30
b)2√15
c)16
d)18
e)6√10

por **Elcioschin** Qua 15 Jul 2020, 13:23

Uma figura para ajudar:

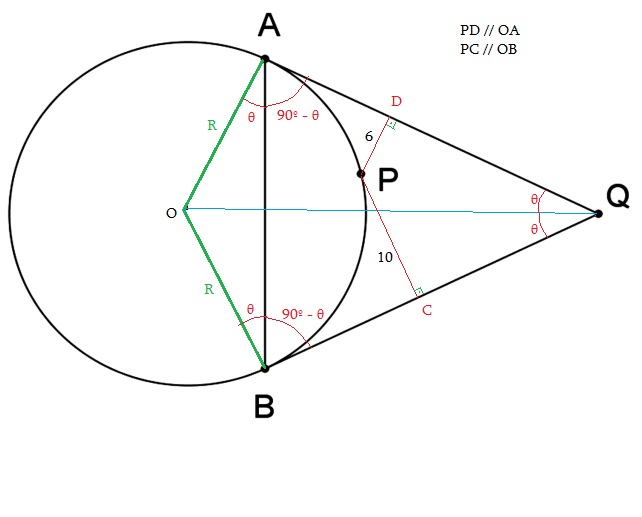
Desafio Matemática(9.1.3): Geometria Plana Pono_p11

por **Medeiros** Qua 15 Jul 2020, 13:44

resp. b) 2√15
vide
https://pir2.forumeiros.com/t103750p15-geometria-plana#360932

por **Medeiros** Qua 15 Jul 2020, 15:59

noto agora que, no link por mim enviado, a figura está cortada. Antigamente este fórum ajustava automaticamente a figura na grade da mensagem, o que nanão acontece mais.

Felizmente ainda tenho o desenho e o vou reenviar. Apenas a nomenclatura dos pontos difere um pouco mas sem impacto sobre compreensão da mecânica de solução.

Desafio Matemática(9.1.3): Geometria Plana Scree880

por Lucius Draco Qua 15 Jul 2020, 22:00

Resolvido!

por Nassif Qui 16 Jul 2020, 14:40

(I) x/6 = b/a -----> x = 6b/a

(II) x/10 = a/b -----> x = 10a/b

(III) 10a/b = 6b/a -----> 6b²=10a²

(IV) a = b√ 6/10

(V) Se x = 10a/b ----> 10/b.b√ 6/√ 10 -----> x = √ 60 ---- > x = 2√ 15

Desafio Matemática(9.1.3): Geometria Plana Semelh10

A... uma dúvida! AB = 2r?

por **Elcioschin** Qui 16 Jul 2020, 14:51

Não. Se fosse, as duas retas tangentes seriam paralelas e não existiria o ponto Q

por **Medeiros** Qui 16 Jul 2020, 15:14

Nassif escreveu:A... uma dúvida! AB = 2r?

Perfeito, Nassif, dados os quatro triângulos semelhantes dois a dois podemos relacionar e obter x sem precisar considerar os outros dois triângulos semelhantes.

Quanto a sua pergunta, veja, na página 1 do link que colei acima, a solução (brilhante) dada pelo colega Raimundo Pereira e as discussões a posteriori -- se der ânimo ainda posto aqui aquela solução de forma mais explicada.

por Nassif Qui 16 Jul 2020, 22:17

Medeiros escreveu:
Nassif escreveu:A... uma dúvida! AB = 2r?

Perfeito, Nassif, dados os quatro triângulos semelhantes dois a dois podemos relacionar e obter x sem precisar considerar os outros dois triângulos semelhantes.

Quanto a sua pergunta, veja, na página 1 do link que colei acima, a solução (brilhante) dada pelo colega Raimundo Pereira e as discussões a posteriori -- se der ânimo ainda posto aqui aquela solução de forma mais explicada.

Opa, valeu !
Com certeza, ser puder, é válido...