Desafio Matemática(9.1.1): Geometria Plana

Continuando com a série de desafios!
(Resposta será postada às 22:00h)

(UFI - 2020)Imagine uma construção feita da seguinte forma:

Constrói-se duas circunferências tangentes externamente entre si e trace a reta tangente entre elas. Como podemos ver na figura a seguir.



A partir dai constrói-se círculos da seguinte forma:

1) Circulo A2, será tangente à A0, A1 e "base".
2) Circulo A3, será tangente à A0, A2 e "base".
3) Circulo A4, será tangente à A0, A3 e "base".
....

Com isso, sabendo que R₀=1cm e R₁=0.25cm, calcule a soma de todos os raios.

Uma figura para ajudar:

Acabou o tempo (Atrasado...)

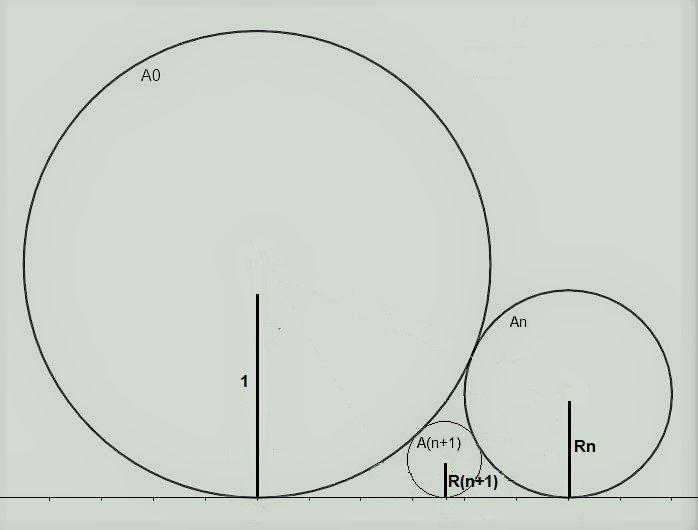
Observe que para com dois círculos quaisquer (como os da figura abaixo) temos:


Por Pitágoras:

[latex]x^2 + (R - r)^2 = (R + r)^2[/latex]

[latex]x = 2\cdot \sqrt{R\cdot r}[/latex]

Com isso, para n ≥ 1, temos:



[latex]2\cdot \sqrt{1\cdot r_{n+1}} + 2\cdot \sqrt{r_{n}\cdot r_{n+1}} = 2\cdot \sqrt{1\cdot r_{n}}[/latex]

[latex]\frac{1}{\sqrt{r_{n}}} + 1 = \frac{1}{\sqrt{r_{n+1}}}\; (P.A.)[/latex]

[latex]\frac{1}{\sqrt{r_{n}}}=n+1[/latex]

[latex]r_{n}= \frac{1}{(n+1)^2}; \: \forall n\geq 1,n\epsilon \mathbb{N}[/latex]

Com isso,

[latex]S = \sum_{n=0}^{\infty }r_{n} = r_{0} + \sum_{n=1}^{\infty }r_{n} = 1 + \sum_{n=1}^{\infty }\frac{1}{(n+1)^{2}} = \sum_{n=0}^{\infty }\frac{1}{(n+1)^{2}}[/latex]

[latex]S = \sum_{n=1}^{\infty }\frac{1}{n^{2}} = \frac{\pi ^{2}}{6}[/latex]