retas

QUESTÃO 143
Um programador visual deseja modificar uma imagem,
aumentando seu comprimento e mantendo sua largura.
As figuras 1 e 2 representam, respectivamente, a imagem
original e a transformada pela duplicação do comprimento.
Figura 1 Figura 2
Para modelar todas as possibilidades de transformação
no comprimento dessa imagem, o programador precisa
descobrir os padrões de todas as retas que contêm os
segmentos que contornam os olhos, o nariz e a boca e,
em seguida, elaborar o programa.
No exemplo anterior, o segmento A1
B1
da figura 1,
contido na reta r1
, transformou-se no segmento A2
B2
da
figura 2, contido na reta r2


.
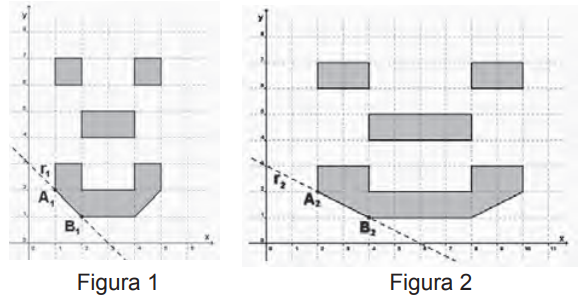
Suponha que, mantendo constante a largura da imagem,
seu comprimento seja multiplicado por n, sendo n um
número inteiro e positivo, e que, dessa forma, a reta r1
sofra as mesmas transformações. Nessas condições, o
segmento An
Bn
estará contido na reta rn
.
A equação algébrica que descreve rn
, no plano
cartesiano, é
A) x + ny = 3n.
B) x − ny = − n.
C) x − ny = 3n.
D) nx + ny = 3n.
E) nx + 2ny = 6n.



C.O.M.O?

Faltou postar as figuras.

Elcioschin escreveu:Faltou postar as figuras.

verdade, já ajeitei, vlw

1) Reta r1 passa por A1(1, 2) e tem coeficiente angular m = -1 

Equação de r1 ---> y - 2 = -1.(x - 1) ---> x + y = 3

2) Reta r2 passa por A2(2, 2) e tem coeficiente angular m = -1/2 

Equação de r2 ---> y - 2 = (-1/2).(x - 2) ---> x + 2.y = 6

3) Reta r3 passa por A3(3, 2) e tem m = -1/3

Equação de r3 ---> y - 2 = (-1/3).(x - 3) ---> x + 3.y = 9

Solução para a reta rn ---> x + n.y = 3.n ---> Alternativa A


Você postou sua questão erradamente em Álgebra: A questão é de Geometria Analítica. Vou mudar mas tome mais cuidado nas próximas postagens.

eita foi mal, é pq eu achava que envolvia só função linear