FME - Quadriláteros Notáveis

por WMaxwell_ Qua 18 Mar 2020, 09:14

Considerando que os segmentos com "marcas iguais" são congruentes, determine os valores das incógnitas, em cada item:
Meu problema está na alternativa "D". Segue imagem:
FME - Quadriláteros Notáveis KXDlcMp

Gabarito: x = 20 y = 6

Meu cálculo:

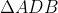
$FME - Quadriláteros Notáveis Gif$ $FME - Quadriláteros Notáveis Gif$

$FME - Quadriláteros Notáveis Gif$ $FME - Quadriláteros Notáveis Gif$

$FME - Quadriláteros Notáveis Gif$

porém não consigo prosseguir a partir daí, fiquei em um "looping". Toda relação que eu tento fazer cai em x = 3y + 2. Eu sei que é uma questão "bobinha", mas gostaria de saber como proceder. Obrigado desde já :/

por **Elcioschin** Qua 18 Mar 2020, 09:52

Você não está respeitando a Regra XI do fórum. O enunciado está incompleto: nem sabemos o que a alternativa D diz. Coloque todas as alternativas.

Propriedades:

1) Base média ---> MN = (AB + CD)/2 ---> MN = (x + y)/2

2) Mediana de Euler ---> PQ = (AB - CD)/2 ---> y + 1 = (x - y)/2

3) Semelhança de triângulos, sendo O o ponto de encontro das diagonais:

ACD semelhante APM
BCD semelhante BNQ
ABO semelhante CDO
ABO semelhante PQO

por WMaxwell_ Qua 18 Mar 2020, 10:04

Elcioschin escreveu:Você não está respeitando a Regra XI do fórum. O enunciado está incompleto: nem sabemos o que a alternativa D diz. Coloque todas as alternativas.

Propriedades:

1) Base média ---> MN = (AB + CD)/2 ---> MN = (x + y)/2

2) Mediana de Euler ---> PQ = (AB - CD)/2 ---> y + 1 = (x - y)/2

3) Semelhança de triângulos, sendo O o ponto de encontro das diagonais:

ACD semelhante APM
BCD semelhante BNQ
ABO semelhante CDO
ABO semelhante PQO

Perdão Elci, eu já corrigi dois erros que havia cometido no enunciado e no título. Quanto ao "nem sabemos o que a alternativa D diz" a questão é assim mesmo, ela te dá vários quadriláteros e pede para encontrar o valor das incógnitas, a questão completa é desnecessária.
A alternativa D é basicamente a imagem que eu anexei.

por WMaxwell_ Qua 18 Mar 2020, 10:08

2) Mediana de Euler ---> PQ = (AB - CD)/2 ---> y + 1 = (x - y)/2

ACD semelhante APM
BCD semelhante BNQ
ABO semelhante CDO
ABO semelhante PQO

Obrigado por citar essa propriedade, eu ainda não a conhecia. Estou no processo de evolução na geometria (área linda Razz

). Vou prosseguir com a questão, obrigado mesmo.

por **Elcioschin** Qua 18 Mar 2020, 10:52

Quando conseguir completar, poste o passo-a-passo da sua solução para que outros usuários aprendam com ela.

por **Rory Gilmore** Qua 18 Mar 2020, 12:42

Você não colocou o enunciado completo da questão, deveria ter citado que a figura corresponde a um trapézio e o segmento MN = x - 2y + 5 !!!!!!!!!!!!

MN = Base média do trapézio = (x + y)/2

MP = base média do triângulo ACD = y/2

PQ = y + 1

QN = base média do triângulo BCD = y/2

I) MN = MP + PQ + QN
(x + y)/2 = y/2 + y + 1 + y/2
(x + y)/2 = 2y + 1
x + y = 4y + 2
x = 3y + 2

II) MN = MP + PQ + QN
x - 2y + 5
x - 2y + 5 = y/2 + y + 1 + y/2
x - 2y + 5 = 2y + 1
x + 5 = 4y + 1
x = 4y - 4

Substituindo x em (I):
3y + 2 = 4y - 4
y = 6

Substituindo y em (II):
x = 4.(6) - 4
x 24 - 4
x = 20

por WMaxwell_ Qua 18 Mar 2020, 13:57

Rory Gilmore escreveu:Você não colocou o enunciado completo da questão, deveria ter citado que a figura corresponde a um trapézio e o seguimento MN = x - 2y + 5 !!!!!!!!!!!!

Caraca, realmente, me passei nesse detalhe... e isso explica meu looping. Perdão pela falta de atenção. Neutral