Números Complexos- (IME-98)

por analuizascrr Sex 10 Jan 2020, 17:07

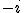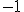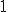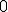Determine os parâmetros $Números Complexos- (IME-98) Mimetex_$ e $Números Complexos- (IME-98) Mimetex_$ da transformação complexa, $Números Complexos- (IME-98) Mimetex_$ , que leva os pontos $Números Complexos- (IME-98) Mimetex_$ $Números Complexos- (IME-98) Mimetex_$ , $Números Complexos- (IME-98) Mimetex_$ para $Números Complexos- (IME-98) Mimetex_$ , $Números Complexos- (IME-98) Mimetex_$ , $Números Complexos- (IME-98) Mimetex_$ , respectivamente, bem como, 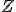$Números Complexos- (IME-98) Mimetex_$ para $Números Complexos- (IME-98) Mimetex_$ , onde $Números Complexos- (IME-98) Mimetex_$ .

não consegui entender o exercício, como assim levar os pontos Z para W? Nunca fiz uma questão parecida. Por favor, me expliquem.

O gabarito traz Z=1+i

por **fantecele** Sex 10 Jan 2020, 23:45

É como se isso ai fosse uma função, uma f(x) por exemplo, se você pega um x qualquer no domínio de f e aplica em f, que no caso seria o f(x), então o ponto que era x passou a ser f(x) depois dessa aplicação, então ele foi levado de x para f(x), acho que foi isso que o exercício quis dizer com essa de levar Z para W.
Aí basta substituir os Z's naquela parte a direita e igualar aos seus respectivos W's, primeiro faça Z = 0 e W = i, depois Z = -i e W = 1 e Z = -1 e W = 0, daí você vai encontrar que α = β = δi e γ = -δ, aparentemente não dá pra encontrar valores exatos para eles, mas tudo bem, daí pra encontrar Z tal que W = -2 - i basta substituir esses valores encontrados ali em cima pra simplificar a função e substituir esse W para encontrar Z, que vai ser 1 + i.
A titulo de curiosidade, creio eu que essa função aí é a Transformação de Mobius.