Função Reciproca

por Luciano Augusto Qui 19 Dez 2019, 17:55

(Mackenzie-SP) A figura ao lado mostra o gráfico da função real definida por f(x) = (ax + b) / (x + c), com a, b, e c números reais. Então f(a + b + c) vale:

{Observação: minha câmera esta ruim, pontilhado corta em x = 1 em y = 3}

a) 1
b) 2
c) 4
d) 5
e) 6

GABARITO: E

Minha resolução:
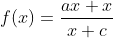
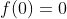
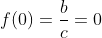
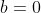
$Função Reciproca Gif$

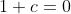
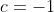
$Função Reciproca Gif$

$Função Reciproca Gif$

$Função Reciproca Gif$

Como x é diferente de 1 então supus que quando x=1 então x+c = 0 pois dará divisão por zero por essa causa
x ≠ 1 (lembrando que eu só supus não tenho certeza se é por isso)

Portanto para x = 1 supus que

$Função Reciproca Gif$

$Função Reciproca Gif$

Nessa parte eu não sei mas como proceder, já "encontrei" o valor de B e C, não sei como encontra A.

por Lucasdeltafisica Qui 19 Dez 2019, 18:19

Fiz da seguinte forma:
Quanto à b
0 = 0 + b/0 +c

B = 0 ~

Quanto à c

Não existe y para 1, e uma fração com denominador nulo não possui significado matemático nos reais.
c + 1 = 0, c = -1

Quanto à a

Quando x tende ao infinito positivo e negativo, y tende à 3
3 = ax/x-1
x(3-a) = 3
3-a = 3/x
3/x com x->infinito = 0
3-a = 0
3 = a

por Luciano Augusto Qui 19 Dez 2019, 18:44

Lucasdeltafisica escreveu:Fiz da seguinte forma:
Quanto à b
0 = 0 + b/0 +c

B = 0 ~

Quanto à c

Não existe y para 1, e uma fração com denominador nulo não possui significado matemático nos reais.
c + 1 = 0, c = -1

Quanto à a

Quando x tende ao infinito positivo e negativo, y tende à 3
3 = ax/x-1
x(3-a) = 3
3-a = 3/x
3/x com x->infinito = 0
3-a = 0
3 = a

Nossa muito obrigado

por Tera Qui 04 Ago 2022, 21:20

Lucasdeltafisica escreveu:Quando x tende ao infinito positivo e negativo, y tende à 3
3 = ax/x-1
x(3-a) = 3
3-a = 3/x
3/x com x->infinito = 0
3-a = 0
3 = a

Não entendi de onde saiu esse x(3-a). Poderia explicar?
Não deveria ser, 3(x-1) = ax?

por **Elcioschin** Qui 04 Ago 2022, 21:46

....... a.x
3 = ------
...... x - 1

3.(x - 1) = a.x ---> 3.x - 3 = a.x ---> 3.x - a.x = 3 ---> (3 - a).x = 3 --->

......... 3
x = --------
...... 3 - a