(CESCEA-71) A solução da inequação sen2x.(sec²x-1/3)≤0
3 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
 (CESCEA-71) A solução da inequação sen2x.(sec²x-1/3)≤0
(CESCEA-71) A solução da inequação sen2x.(sec²x-1/3)≤0
Edit 1:(CESCEA-71) A solução da inequação sen2x.(sec²x-1/3) ≤ 0 no intervalo fechado [0, 2\pi ] é:

Edit 2: o gabarito do livro (FME) indica a letra b, mas achei um outro tópico no fórum e as resoluções apresentadas foram condizentes com a minha resolução, que eu acreditava estar errada. Acredito ser a letra D a correta.

Edit 2: o gabarito do livro (FME) indica a letra b, mas achei um outro tópico no fórum e as resoluções apresentadas foram condizentes com a minha resolução, que eu acreditava estar errada. Acredito ser a letra D a correta.
- Spoiler:
- Resolução:
I) sen(2x) = 2senx.cosx. O produto será positivo quando houver sinais iguais.
Logo, sen2x será positivo com x no 1º (senx e cosx positivos) e no 3º quadrante (senx e cosx negativos) e negativo no 2º e 4º
II) sec²x-1/3 = 1/cos²x - 1/3
cosx=[-1,1] e cosx≠0 (já que o denominador ≠ 0)
Portanto, 1/cos²x - 1/3 sempre será maior que 0, já que 0 < cos²x ≤1
Quadro de sinais: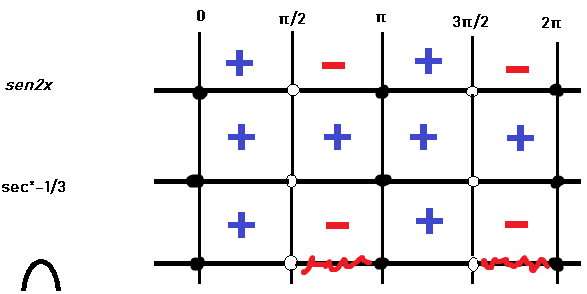
Alternativa D)
Última edição por Milico em Sáb 09 Nov 2019, 18:06, editado 5 vez(es)
Milico- Iniciante
- Mensagens : 18
Data de inscrição : 09/11/2019
Idade : 23
Localização : Campinas-SP
 Re: (CESCEA-71) A solução da inequação sen2x.(sec²x-1/3)≤0
Re: (CESCEA-71) A solução da inequação sen2x.(sec²x-1/3)≤0
Bem-vindo ao fórum.
Para ser bem atendido você precisa conhecer e seguir nossas Regras (no alto desta página).
Nesta postagem você desrespeitou a Regra IX: o texto do enunciado deve ser digitado.
Por favor, EDITe sua mensagem original, digitando o texto (sinais ≤ , ≥ , π existem na tabela ao lado SÍMBOLOS ÚTEIS).
E, por favor, leia todas as Regras e siga-as as próximas postagens.
Para ser bem atendido você precisa conhecer e seguir nossas Regras (no alto desta página).
Nesta postagem você desrespeitou a Regra IX: o texto do enunciado deve ser digitado.
Por favor, EDITe sua mensagem original, digitando o texto (sinais ≤ , ≥ , π existem na tabela ao lado SÍMBOLOS ÚTEIS).
E, por favor, leia todas as Regras e siga-as as próximas postagens.

Elcioschin- Grande Mestre

- Mensagens : 73189
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP

SnoopLy- Jedi

- Mensagens : 225
Data de inscrição : 23/02/2017
Idade : 24
Localização : Brasil, Rio de Janeiro
 Tópicos semelhantes
Tópicos semelhantes» Solução da Inequação
» Solução da inequação
» Inequação solução
» Solução da inequação
» Solução p/ Inequação
» Solução da inequação
» Inequação solução
» Solução da inequação
» Solução p/ Inequação
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













