Arco e circunferência

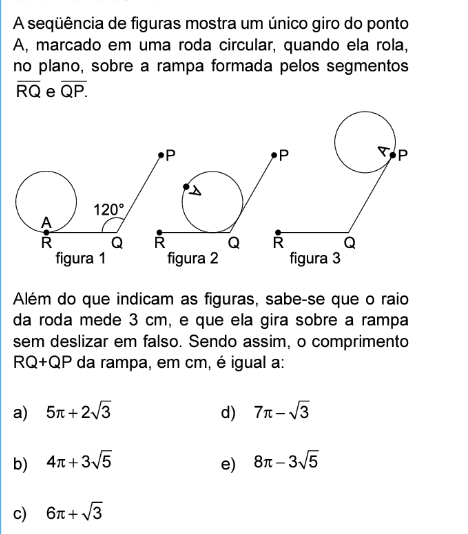
qüência  de  figuras  mostra  um  único  giro  do  ponto A,  marcado  em  uma  roda  circular,  quando  ela  rola, no  plano,  sobre  a  rampa  formada  pelos  segmentos RQ e QP.
Além  do  que  indicam  as  figuras,  sabe-se  que  o  raio da  roda  mede  3  cm,  e  que  ela  gira  sobre  a  rampa sem  deslizar  em  falso.  Sendo  assim,  o  comprimento RQ+QP da rampa, em cm, é igual a:
a) 5π+2√3
 b) 4π+3√5 
c)6π+√3
d) 7π-√3
e)8π−3√5

Gabarito: A

O comprimento que a roda toca o solo é: (5/6)*2.pi.r = 5.pi

A parte da rampa que é "pulada" pela roda é:
2* 3/(tg60°) = 2*√3

.:. toda a rampa mede: 5.pi + 2√3


Obs: agora estou no celular, em viagem. Chegando em casa explico melhor, com desenho.

continuando...

Seja O o centro do círculo, e B e C os pontos de tangência com o segmento quebrado assinalados no desenho.

Se o círculo rodasse sobre um segmento de reta o comprimento de tal segmento seria o mesmo da circunferência: 2.π.r
Porém este é um segmento quebrado, que forma um ângulo interno de 120°, e a circunferência não consegue tocar em toda a sua extensão.
O que acontece é que o círculo roda de A até B -- tocando o segmento de R até Q -- e depois completa a volta rodando de C até A -- e tocando o segmento de C até P. Portanto a circunferência "pula" o arco menor \overarc{BC}



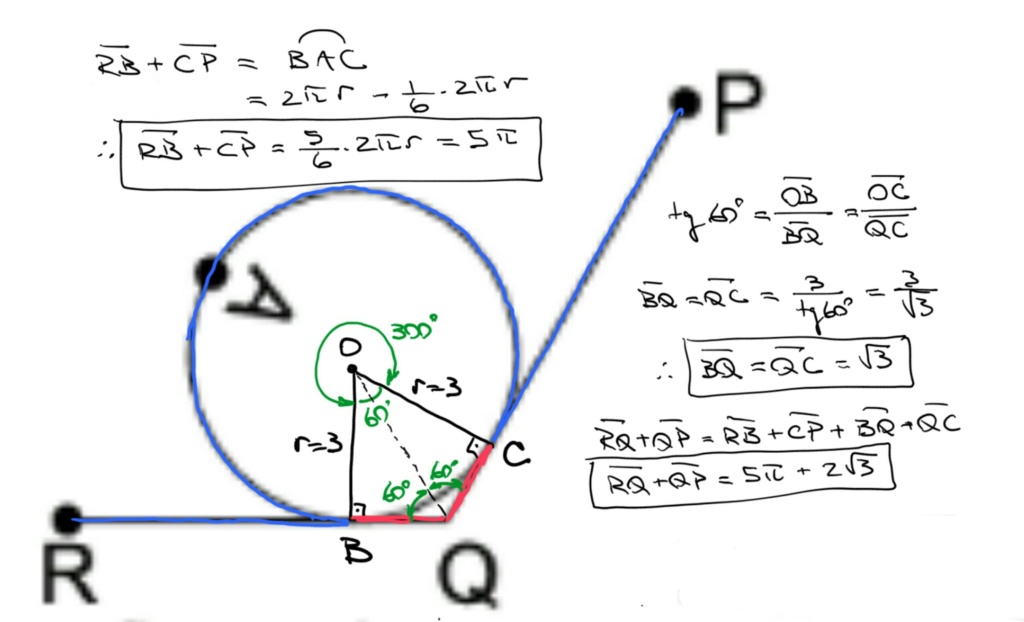
A soma dos ângulos internos de um quadrilátero é 360° e o quadrilátero OBQC tem dois ângulos de 90° (na tangência com o raio) e um ângulo de 120° (\angle BQC); portanto \angle BOC = 60°.

Como 60° é 1/6 da circunferência -- e esta é justamente a parte que ela "pula" o contato com o segmento -- a parte da circunferência que adere ao segmento, e portanto nos dá a medida do segmento RB+CP, é 5/6 do comprimento da circunferência.

No quadrilátero OBQC, traçando-se OQ o dividimos em dois triângulos retângulos congruentes. Portanto o ângulo de 120° fica dividido ao meio. E através da tangente de 60° podemos calcular BQ e QC.

Muito obrigada!