Arco AB
2 participantes
Página 1 de 1
Arco AB
por Zeis Ter 11 Jan 2022, 13:14
1. Um arco AB tem comprimento 80cm e as tangentes em A e B formam um ângulo de 144°. Calcule a área do círculo em função da corda AB.
Zeis- Mestre Jedi
- Mensagens : 530
Data de inscrição : 16/03/2020
Re: ARCO AB
por João Pedro Lima Ter 25 Jan 2022, 18:37
Fala, Zeis.
Seguinte:
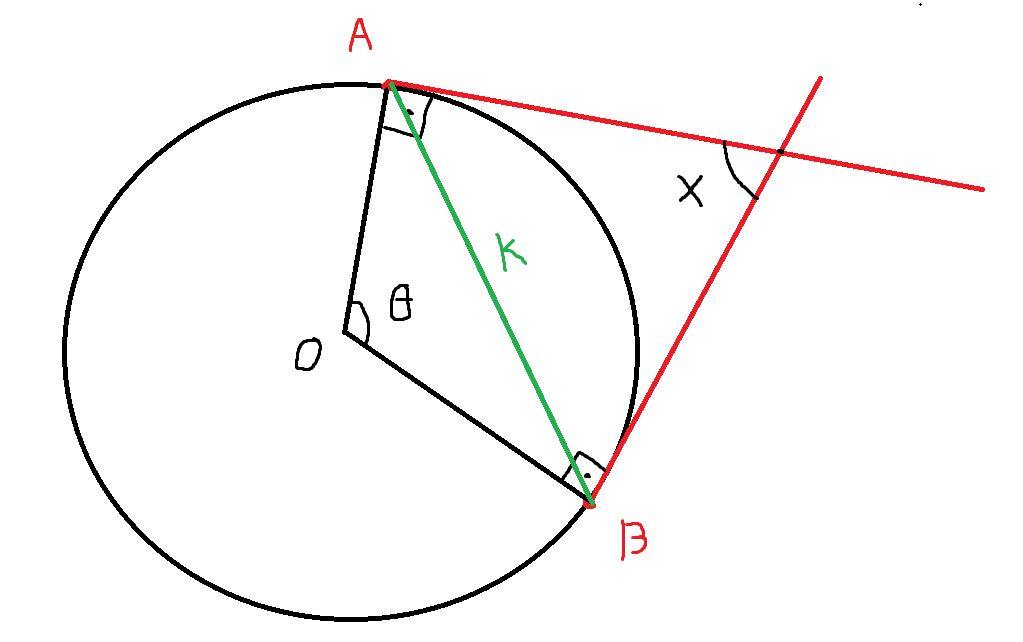
A questão não especificou onde o ângulo de 144 graus se localiza, repare que x = 144 ou 180 - 144. Por isso, farei apenas em função de x.
Como as tangentes fazem um angulo de noventa graus com os raios, temos que x + θ = 180 graus -> θ = 180 - x.
Lei dos cossenos em AOB:
[latex]K^2 = 2R^2 + 2R^2cos\theta[/latex]
[latex]K = R\sqrt{2-2cos\theta}[/latex]
[latex]K = R\sqrt{2-2cos(180-x)}[/latex]
Logo:
[latex]\frac{K}{\sqrt{2-2cos(180-x)}} = R[/latex]
[latex]\frac{K^2}{2-2cos(180-x)} = R^2[/latex]
[latex]\frac{K^2}{2-2cos(180-x)}.\pi = R^2.\pi[/latex]
Seguinte:
A questão não especificou onde o ângulo de 144 graus se localiza, repare que x = 144 ou 180 - 144. Por isso, farei apenas em função de x.
Como as tangentes fazem um angulo de noventa graus com os raios, temos que x + θ = 180 graus -> θ = 180 - x.
Lei dos cossenos em AOB:
[latex]K^2 = 2R^2 + 2R^2cos\theta[/latex]
[latex]K = R\sqrt{2-2cos\theta}[/latex]
[latex]K = R\sqrt{2-2cos(180-x)}[/latex]
Logo:
[latex]\frac{K}{\sqrt{2-2cos(180-x)}} = R[/latex]
[latex]\frac{K^2}{2-2cos(180-x)} = R^2[/latex]
[latex]\frac{K^2}{2-2cos(180-x)}.\pi = R^2.\pi[/latex]
João Pedro Lima- Jedi
- Mensagens : 220
Data de inscrição : 02/01/2022
Idade : 22
Localização : Rio de Janeiro, RJ
Tópicos semelhantes» Equação com arco-tangente e arco-cotangente
» Explicação, por que o arco-íris é um arco?
» Arco BC
» arco TP
» Arco.
» Explicação, por que o arco-íris é um arco?
» Arco BC
» arco TP
» Arco.
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
