área de triângulo

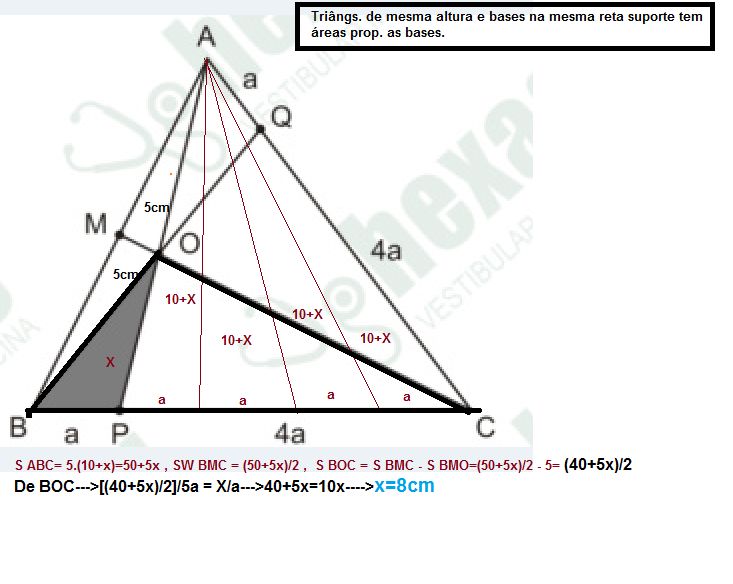
(Insper) No triângulo ABC da figura, M é ponto médio de AB e P e Q são pontos dos lados BC e AC, respectivamente, tais que BP=AQ=a e PC=QC=4a.




Os segmentos AP, BQ e CM Interceptam-se no ponto O e a área do triângulo BOM é 5 cm². Dessa forma, a área do triângulo BOP, assinalado na figura, é igual a: 

a) 5 cm² 
b) 6 cm² 
c) 8 cm² 
d) 9cm²
e) 10 cm

Spoiler:

I) O triângulo ABC é isósceles de base AB e a mediana CM é altura relativa a base.

II) De I concluímos que os triângulos BOM e AOM são retângulos e congruentes.

III)De II concluímos que os triângulos BOP e AOQ são congruentes.

IV) De III concluímos que os triângulos POC e QOC são congruentes.

V) Os triângulos POC e QOC têm o quádruplo da área dos triângulos BOP e AOQ, porque possuem a mesma altura que é relativa aos lados a e 4a e a base é o quádruplo da base de AOQ.

VI) Seja S a área de BOP e AOQ, o triângulo APB tem área igual a S + 10 ou então a.h/2 onde h é altura relativa a BC.

VII) O triângulo ABC tem área igual a 10S + 10 ou então 5a.h/2
10S + 10 = 5a.h/2
2S + 2 = a.h/2

Da relação VI:

S + 10 = a.h/2
S + 10 = 2S + 2
S = 8 cm²

Não entendi VII, Rory. 
Ccomo você colocou 10S + 10 (área de ABC) em função de h, se não é essa a altura dele?
Eu entendi que S + 10 = a.h/2, mas se eu fosse substituir, não  seria outra equação?

O colega Rory Gilmore chamou de h a distância do ponto O ao lado BC:

Elcioschin, na verdade eu chamei de h a altura do triângulo ABC relativa ao lado BC.

Raquel Valadão, você consegue ver que essa altura relativa ao lado BC no triângulo ABC é a mesma relativa ao lado BP no triângulo APB (destaquei ela em vermelho na imagem do final)?

Daí decorre que a área de ABC pode ser escrita como: BC.h/2 = 5a.h/2
Daí decorre também que a área de APB pode ser escrita como BP.h/2 = a.h/2

Mas como já sabíamos que a área de ABC é 10S + 10, temos:
10S + 10 = 5a.h/2
2S + 2 = a.h/2

E como também sabíamos que a área de APB é S + 10, temos:
S + 10 = a.h/2 

Substituindo na expressão 2S + 2 = a.h/2:
2S + 2 = S + 10
S = 8 cm²

Tens razão Rory Gilmore: h é a altura do triângulo APB, relativa à sua base BP, conforme a sua figura em vermelho (o meu h, em verde, é a altura do triângulo OBP em relação à base BP).