Cilindro
2 participantes
Página 1 de 1
Cilindro
por melissa_miranda Seg 17 Jun 2019, 09:01
2. Seja r uma constante positiva. Considere o cilindro x2 + y2 ≤ r2, e seja C a parte do cilindro que satisfaz 0 ≤ z ≤ y.
(1) Considere a seção transversal de C pelo plano x = t (r ≤ t ≤ r),
e expressar sua área em termos de r, t.
Antecipadamente grata! Pois preciso muito de ajuda nessa.e expressar sua área em termos de r, t.
- Spoiler:
- (r²-t²)/2
Última edição por melissa_miranda em Sex 21 Jun 2019, 10:34, editado 1 vez(es)
melissa_miranda- Recebeu o sabre de luz
- Mensagens : 118
Data de inscrição : 15/01/2019
Idade : 24
Localização : Pirapora - Minas Gerais, Brasil
Re: Cilindro
por mauk03 Qua 19 Jun 2019, 01:32
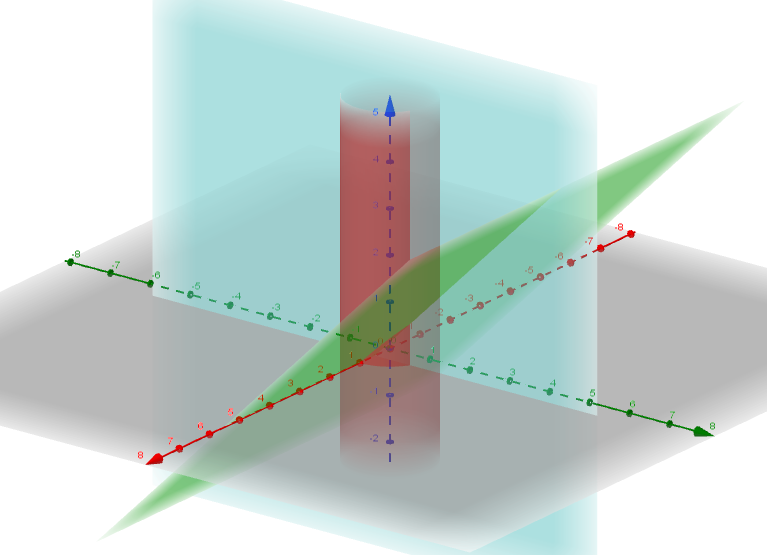
(Obs.: Cilindro em vermelho, plano z = y em verde e plano x = t em azul)
A região de intersecção é onde o plano x = t corta a parte do cilindro abaixo do plano z = y e acima do plano z = 0 (plano cinza na imagem). Observe que essa região é um triângulo retângulo isósceles (pois o plano z = y forma ângulo de 45º com o plano z = 0) cuja base e altura são iguais a distância entre a intersecção do plano x = t com o eixo x (ponto (t, 0, 0)) e a intersecção do plano x = t com o cilindro no plano z = 0 (ponto (t, √(r² - t²), 0)). Assim:
Área = (1/2)*base*altura = (1/2)*√(r² - t²)*√(r² - t²) = (r² - t²)/2
mauk03- Fera
- Mensagens : 831
Data de inscrição : 14/04/2012
Idade : 31
Localização : TB - Paraná - Br
melissa_miranda- Recebeu o sabre de luz
- Mensagens : 118
Data de inscrição : 15/01/2019
Idade : 24
Localização : Pirapora - Minas Gerais, Brasil
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
