UDESC- Triângulos
3 participantes
Página 1 de 1
UDESC- Triângulos
por Lord Stark Qui 30 maio 2019, 23:25
Em um triângulo retângulo ABC são construídos três triângulos equiláteros, conforme a figura.
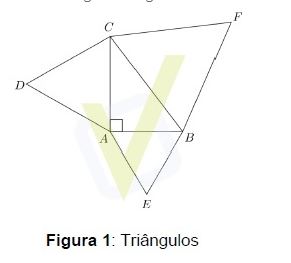
Com base na informação e na figura, análise as proposições.
I. A soma das áreas dos triângulos ACD e ABE é igual à área do triângulo CBF.
II. Se a área do triângulo ABC é 6 cm² e altura do triângulo CBF é √30 cm, então o perímetro do triângulo ABC é 2( 4 + √10) cm.
III. Se o triângulo ABC for isósceles, então a soma dos comprimentos dos segmentos BE e BF é igual ao comprimento do segmento DE.
Assinale a alternativa correta.
a) Somente as afirmativas II e III são verdadeiras
b) Somente a afirmativa I é verdadeira
c) Somente as afirmativas I e II são verdadeiras
d) Somente a afirmativa II é verdadeira
e) Somente as afirmativas I e III são verdadeiras
Com base na informação e na figura, análise as proposições.
I. A soma das áreas dos triângulos ACD e ABE é igual à área do triângulo CBF.
II. Se a área do triângulo ABC é 6 cm² e altura do triângulo CBF é √30 cm, então o perímetro do triângulo ABC é 2( 4 + √10) cm.
III. Se o triângulo ABC for isósceles, então a soma dos comprimentos dos segmentos BE e BF é igual ao comprimento do segmento DE.
Assinale a alternativa correta.
a) Somente as afirmativas II e III são verdadeiras
b) Somente a afirmativa I é verdadeira
c) Somente as afirmativas I e II são verdadeiras
d) Somente a afirmativa II é verdadeira
e) Somente as afirmativas I e III são verdadeiras
Lord Stark- Jedi
- Mensagens : 218
Data de inscrição : 16/07/2017
Idade : 27
Localização : Caxias-MA
Re: UDESC- Triângulos
por Elcioschin Sex 31 maio 2019, 00:15
I) Sejam AB = c , AC = b , BC = a ---> b² + c² = a²
S(ACD) = b².√3/4 ---> S(ABE) = b².√3/4 ---> S(BCF) = a².√3/4
b².√3/4 + b².√3/4 = b².√3/4 ---> : √3/4 ---> b² + c² = a² ---> OK
II) S(ABC) = 6 ---> b.c/2 = 6 ---> b.c = 12 ---> I
h = BC.√3/2 ---> √30 = a.√3/2 ---> a = 2.√10 ---> b² + c² = 40 ---> b² + 2.b.c + c² = 40 + 2.b.c --->
(b + c)² = 40 + 2.b.c ---> II
I em II ---> (b + c)² = 40 + 2.12 ---> (b + c)² = 64 ---> b + c = 8 ---> c = 8 - b --->III
III em I ---> b.(8 - b) = 12 ---> b² - 8.b + 12 = 0 ---> b = 6 ou b = 2
Pela figura ---> b = 6 ---> c = 2
p(ABC) = b + c + a = 6 + 2 + 2.√10 = 2.(4 + √10) ---> OK
III) b = c ---> DÂE = 150º (360º - 90º - 60º - 60º)
DE² = AD² + AE² - 2.AD.AE.cos150º ---> DE² = b² + b² - 2.b².(-√3/2)
Complete
S(ACD) = b².√3/4 ---> S(ABE) = b².√3/4 ---> S(BCF) = a².√3/4
b².√3/4 + b².√3/4 = b².√3/4 ---> : √3/4 ---> b² + c² = a² ---> OK
II) S(ABC) = 6 ---> b.c/2 = 6 ---> b.c = 12 ---> I
h = BC.√3/2 ---> √30 = a.√3/2 ---> a = 2.√10 ---> b² + c² = 40 ---> b² + 2.b.c + c² = 40 + 2.b.c --->
(b + c)² = 40 + 2.b.c ---> II
I em II ---> (b + c)² = 40 + 2.12 ---> (b + c)² = 64 ---> b + c = 8 ---> c = 8 - b --->III
III em I ---> b.(8 - b) = 12 ---> b² - 8.b + 12 = 0 ---> b = 6 ou b = 2
Pela figura ---> b = 6 ---> c = 2
p(ABC) = b + c + a = 6 + 2 + 2.√10 = 2.(4 + √10) ---> OK
III) b = c ---> DÂE = 150º (360º - 90º - 60º - 60º)
DE² = AD² + AE² - 2.AD.AE.cos150º ---> DE² = b² + b² - 2.b².(-√3/2)
Complete
Elcioschin- Grande Mestre
- Mensagens : 73176
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
!!!
Lord Stark- Jedi
- Mensagens : 218
Data de inscrição : 16/07/2017
Idade : 27
Localização : Caxias-MA
Re: UDESC- Triângulos
por Medeiros Sáb 01 Jun 2019, 23:53
A III somente será verdadeira se o triângulo ABC for isósceles de pernas AC=BC, para quaisquer outros casos é falsa. Portanto, não é sempre verdadeira, logo é falsa.
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Tópicos semelhantes» Triângulos - UDESC(2014)
» (UFMG-97) Observe a figura.... semelhança de triângulos e triângulos retângulos.
» (UFMG) - Semelhança de triângulos e triângulos retângulos.
» (UDESC-SC-010) MUV
» UDESC mcu
» (UFMG-97) Observe a figura.... semelhança de triângulos e triângulos retângulos.
» (UFMG) - Semelhança de triângulos e triângulos retângulos.
» (UDESC-SC-010) MUV
» UDESC mcu
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
