Quadrado inscrito na circunferencia

Considere o quadrado ABCD, cujo lado mede 5cm, e M um ponto sobre o círculo circunscrito a este quadrado, não coincidente com os vértices A, B, C e D, conforme ilustra a figura a seguir. Qual o valor da soma (MA)² + (MB)² + (MC)² + (MD)²



(A) 10
(B) 10√2 
(C) 50 
(D) 50√2 
(E) 100 

Sugestão: desenhe as diagonais do quadrado.

Apenas por plana:
Observe, inicialmente temos: 

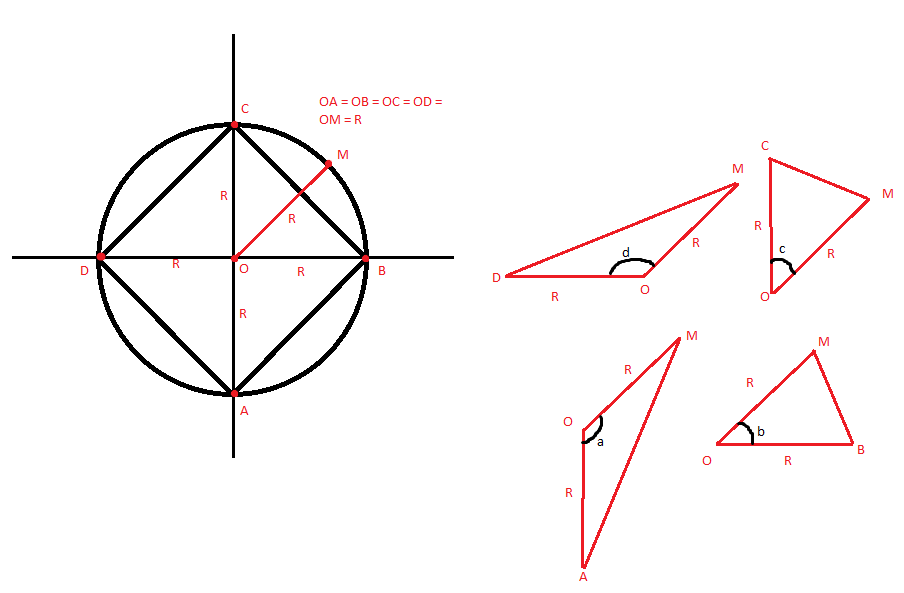
Inicialmente, é óbvio que a diagonal do quadrado de lado 5 é 5raiz(2), e o raio é a metade da diagonal, ou seja, 5raiz(2)/2. Chamarei Raio de R e substituiremos no fim.
Por Lei dos Cossenos, temos MA² = 2R²-2R²cosa, MB² = 2R²-2R²cosb, MC² = 2R²-2R²cosc e MD² = 2R²-2R²cosd
Fazendo a soma e trabalhando a expressão, temos MA²+MB²+MC²+MD² = 2R²[4-(cosa+cosb+cosc+cosd)]
Precisamos achar cosa+cosb+cosc+cosd. Analisemos os angulos no circulo:

É visível que: 
b + c = pi/2     (III)
a = b + pi/2    (I)
d = c + pi/2     (II)


Somando (I) e (II):
a+d = b+c + pi        Usando (III):    
a+d = 3pi/2


Agora vamos achar o que queríamos, cosa+cosb+cosc+cosd    usando (I) e (II):
cos(b+pi/2)+cosb+cosc+cos(c+pi/2)
Veja que cos(b+pi/2),cos(c+pi/2) = -senb, -senc
-senb+cosb+cosc-senc       Porém, por (III), sabemos que senb=cosc e senc=cosb, logo:
-cosc+cosb+cosc-cosb = 0
Portanto, MA²+MB²+MC²+MD² = 2R²(4-0) = 8R² = 8(5raiz(2)/2)² = 100

Generalização: Perceba que para qualquer M na circunferência não coincidente com os vértices, isso será verdade, apesar de eu ter usado um M específico para os cálculos. Qualquer M no primeiro quadrante seria idêntico. Já para um M no segundo quadrante, por exemplo, teríamos d+c=pi/2, b=c+pi/2 e a=d+pi/2. Se mudar para outro quadrante, as equações dos angulos mudam de nome, mas o resultado cosa+cosb+cosc+cosd sempre será 0.

Poderias fazer por analítica também, achando as coordenadas de M em função de R e os angulos b e c, e sabendo, claro, que b+c=pi/2. Recomendo tentar fazer, pra praticar, e quem sabe postar aqui para os colegas forumeiros.

Obrigada pela resposta é sugestão, tentarei fazer aqui

GBRezende escreveu:Poderias fazer por analítica também, achando as coordenadas de M em função de R e os angulos b e c, e sabendo, claro, que b+c=pi/2. Recomendo tentar fazer, pra praticar, e quem sabe postar aqui para os colegas forumeiros.

Ótimo!!

Rory Gilmore escreveu: