Função trigonométrica

por lcvf9696 Qua 20 Mar 2019, 00:37

Determine o valor máximo de 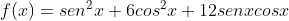$Função trigonométrica Gif$

A) 14 B) 13 C) 12 D) 11 E) 10

Gab:E

por **fantecele** Qua 20 Mar 2019, 16:23

$\\f(x)=sen^2(x) + 6cos^2(x) + 12.sen(x).cos(x)\\f(x)=1 + 5.cos^2(x) + 6.2.sen(x).cos(x)\\f(x)=1 + 5.\frac{cos(2x) + 1}{2} + 6.sen(2x)\\f(x)=1 + \frac{5.cos(x)}{2} + \frac{5}{2} + 6.sen(2x)\\f(x)=\frac{7}{2} + \frac{5.cos(2x) + 12.sen(2x)}{2}$

Considere k um ângulo tal que sen(k) = 5/13 e cos(k) = 12/13, dessa forma:

$\\f(x)=\frac{7}{2} + \frac{5.cos(2x) + 12.sen(2x)}{2}\\\\f(x)=\frac{7}{2}+13.\left (\frac{\frac{5}{13}.cos(2x) + \frac{12}{13}.sen(2x)}{2} \right )\\f(x)=\frac{7}{2}+13.\left (\frac{sen(k).cos(2x) + cos(k).sen(2x)}{2} \right )\\f(x)=\frac{7}{2}+13.\left (\frac{sen(2x+k)}{2} \right )$

Perceba ainda que temos -1 ≤ sen(2x+k) ≤ 1, e, portanto, para que f(x) seja máxima, devemos ter sen(2x+k) igual a 1, portanto o seu valor máximo será:

f(x) = 7/2 + 13/2 = 10

por lcvf9696 Qua 20 Mar 2019, 17:06

Muito boa sua resolução!Obrigado!

por **Giovana Martins** Qua 20 Mar 2019, 17:09

Hoje mais cedo eu tentei reduzir a expressão em algo do tipo asen(u)+bcos(u), mas não estava conseguindo Razz

. Obrigada, fantecele.

Vou deixar apenas uma saída alternativa para o finzinho da resolução. Pela Desigualdade de Cauchy-Scharwz:

\\\left ( 5^2+12^2 \right )\left ( sen^2(2x)+cos^2(2x) \right )\geq \left ( 12sen(2x)+5cos(2x) \right )^2\\\\\left ( 12sen(2x)+5cos(2x) \right )^2\leq 169\to |12sen(2x)+5cos(2x)|\leq 13\\\\\therefore \ -13\leq 12sen(2x)+5cos(2x)\leq 13\\\\\therefore \ f_{max}=\frac{7}{2}+\frac{13}{2}=10\ \wedge\ f_{min}=\frac{7}{2}-\frac{13}{2}=-3

Lcvf, caso você não conheça, o que o colega fantecele fez foi usar o truque do triângulo retângulo.

https://pir2.forumeiros.com/t150465-o-truque-do-triangulo-retangulo