números complexos ( UESB- 2019)

por os_hiago2 Seg 11 Mar 2019, 10:19

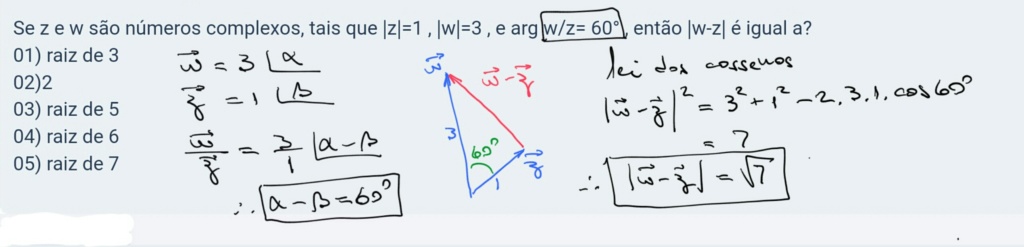
Se z e w são números complexos, tais que |z|=1 , |w|=3 , e arg w/z= 60° , então |w-z| é igual a?
01) raiz de 3
02)2
03) raiz de 5
04) raiz de 6
05) raiz de 7

por **Elcioschin** Seg 11 Mar 2019, 22:33

z = a + b.i ---> |z| = √(a² + b²) ---> a² + b² = 1

w = x + y.i ---> ---> |w| = √(x² + y²) ---> x² + y² = 9

w/z = (x + y.i)/(a + b.i) ----> w/z = (x + y.i).(a - b.i)/(a + b.i).(a - b.i)

w/z = [(a.x + b.y) + (a.y - b.x).i]/(a² + b²) --->

w/z = (a.x + b.y)/(a + b²) + [(a.y - b.x)/(a² + b²)].i

tgθ = parte imaginária/parte real ---> tgθ = (a.y - b.x)/(a.x + b.y) --->

θ = arctg[(a.y - b.x)/(a.x + b.y)] --> 60º = pi/3 --> arctg[(a.y - b.x)/(a.x + b.y)] = pi/3

Tente completar