conjunto imagem

Um outro jeito (usando gráficos).

Pensemos na função y=sec(x).



Quando a função secante está elevada a expoentes pares, a porção dessa curva que está na região abaixo do eixo x é rebatida simetricamente ao eixo x na parte superior desse eixo. Construa, por exemplo, o gráfico de y=sec²(x) para confirmar.

É fácil ver que, conforme aumentamos o expoente "n", a curva y=secⁿ(x), em que "n" é um número par, sofre um estreitamento. Assim, para qualquer "n" par, a função y=g(x)=secⁿ(x) terá imagem Im(g)=[1,+∞[.

Agora, vamos pensar na função y=tg(x).



Utilizando-se o mesmo raciocínio que o anterior, note que, ao elevarmos a função tangente a um expoente par, a porção da curva tangente abaixo do eixo x é rebatida simetricamente ao eixo x na parte superior desse eixo. Construa, por exemplo, o gráfico de y=tg²(x) para confirmar.

Também é fácil ver que, conforme aumentamos o expoente "n", a curva y=tgⁿ(x), em que "n" é um número par, sofre um estreitamento. Assim, para qualquer "n" par, a função y=h(x)=tgⁿ(x) terá imagem Im(h)=[0,+∞[.

Agora, pensemos juntamente nas funções g(x)=secⁿ(x) e h(x)=tgⁿ(x) para "n" par e também em f(x)=(g+h)(x)=g(x)+h(x).



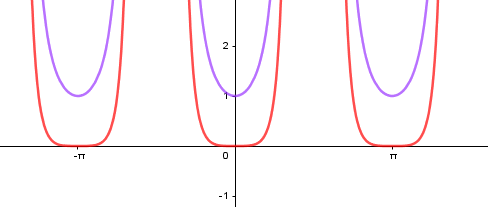
Observe que nas vizinhanças de x=0 (tanto à esquerda quanto à direita), a curva g(x) predomina sobre a curva h(x), isto é, a curva g(x)=secⁿ(x) está acima de h(x)=tgⁿ(x).

Assim, a conformação da curva resultante de f(x)=(g+h)(x)=g(x)+h(x) terá as características de g(x).

Para x=kπ, k ∈ ℤ: f(kπ)=g(kπ)+h(kπ)=1.

Assim, a imagem de f(x) corresponde a Im(f)=[1,+∞[.

Gráfico de y=secⁿ(x)+tgⁿ(x), para "n" par.