imagem do conjunto
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
imagem do conjunto
por NATHGOOL Sex 15 Abr 2016, 09:00
(ITA 1997) Seja n ∈ ℕ, com n >1 fixado. Considere o conjunto
Definimos f:ℝ → ℝ por f(x)=[cos(n!.π.x)]2n
Se f(A) denota a imagem do conjunto A pela função f, então
A( )f(A) = ]—1.1[.
B( )f(A)=[0,1].
C( )f(A)={1}
D( )f(A)={0}
E( )f(A)={0,1}.
LETRA C
MUITO OBRIGADA
.
Definimos f:ℝ → ℝ por f(x)=[cos(n!.π.x)]2n
Se f(A) denota a imagem do conjunto A pela função f, então
A( )f(A) = ]—1.1[.
B( )f(A)=[0,1].
C( )f(A)={1}
D( )f(A)={0}
E( )f(A)={0,1}.
LETRA C
MUITO OBRIGADA
.
NATHGOOL- Jedi
- Mensagens : 200
Data de inscrição : 19/04/2013
FirmusBellus gosta desta mensagem
Re: imagem do conjunto
por Carlos Adir Sex 15 Abr 2016, 20:59
Temos que:
=f\left(\dfrac{p}{q}\right)=\left(cos\left(n!\cdot&space;\pi&space;\cdot&space;\frac{p}{q}&space;\right&space;)&space;\right&space;)^{2n}} "\mathrm{f(A)=f\left(\dfrac{p}{q}\right)=\left(cos\left(n!\cdot \pi \cdot \frac{p}{q} \right ) \right )^{2n}}")
Como q é sempre menor que n, então em algum momento, temos:
\cdots&space;(n-(q-1))\cdot&space;\left(n-(q+1)&space;\right&space;)\cdots&space;\cdot&space;2&space;\cdot&space;1} "\mathrm{\dfrac{n!}{q}=n\cdot (n-1)\cdots (n-(q-1))\cdot \left(n-(q+1) \right )\cdots \cdot 2 \cdot 1}")
Ou seja, a expressão é sempre inteira. Podemos tomar então:
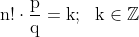
Isso é, a expressão é inteira, logo:
=\left[cos\left(k\cdot&space;\pi&space;\right&space;)&space;\right&space;]^{2n}=\left[(-1)^{k}&space;\right&space;]^{2n}=1} "\mathrm{f(A)=\left[cos\left(k\cdot \pi \right ) \right ]^{2n}=\left[(-1)^{k} \right ]^{2n}=1}")
Usei a relação que cos(k*pi)=(-1)^(k) pois se k=0, então cos(k*pi)=1; se k=1, cos(k*pi)=-1, se k=2 então cos(k*pi)=1, e assim vai. Ou seja, o sinal fica alternando.
Isso só vale porque k é inteiro.
Como q é sempre menor que n, então em algum momento, temos:
Ou seja, a expressão é sempre inteira. Podemos tomar então:
Isso é, a expressão é inteira, logo:
Usei a relação que cos(k*pi)=(-1)^(k) pois se k=0, então cos(k*pi)=1; se k=1, cos(k*pi)=-1, se k=2 então cos(k*pi)=1, e assim vai. Ou seja, o sinal fica alternando.
Isso só vale porque k é inteiro.
____________________________________________
← → ↛ 
⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ º ª ⁿ ⁱ
₀ ₁ ₂ ₃ ₄ ₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ₐ ₑ ₒ ₓ ₔ
∴ ≈ ≠ ≡ ≢ ≤ ≥ × ± ∓ ∑ ∏ √ ∛ ∜ ∝ ∞
∀ ∃ ∈ ∉ ⊂ ⊄ ⋂ ⋃ ∧ ∨ ℝ ℕ ℚ ℤ ℂ
⊥ ║ ∡ ∠ ∢ ⊿ △ □ ▭ ◊ ○ ∆ ◦ ⊙ ⊗ ◈
Αα Ββ Γγ Δδ Εε Ζζ Ηη Θθ Ιι Κκ Λλ Μμ Νν Ξξ Οο Ππ Ρρ Σσς Ττ Υυ Φφ Χχ Ψψ Ωω ϑ ϒ ϖ ƒ ij ℓ
∫ ∬ ∭ ∳ ∂ ∇
ℛ ℜ ℰ ℳ ℊ ℒ
Carlos Adir- Monitor
- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
NATHGOOL- Jedi
- Mensagens : 200
Data de inscrição : 19/04/2013
Tópicos semelhantesPiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
