Em um círculo de raio R inscreve-se...

por Lele9898 Seg 19 Nov 2018, 21:00

Em um círculo de raio R inscreve-se um triângulo equilátero de área 1 cm^2. Em um círculo de raio 4R inscreve-se um hexágono cuja área, em cm^2, é igual a:

A)4 B)8 C)16 D)32 E)64

Gostaria da resolução, por gentileza. Gabarito letra D.

por **Elcioschin** Seg 19 Nov 2018, 21:45

Lado do triângulo equilátero = L ---> L = R.√3

St = L².√3/4 ---> 1 = (R.√3)².√3/4 ---> 4 = 3.√3.R² ---> R² = 4.√3/9

Lado do hexágono = L' ---> L' = R' ---> L' = 4.R

Sh = 6.L'².√3/4 ---> S = 6.(4.R)².√3/4 ---> S = 24.(4.√3/9).√3 ---> S = 32 cm²

por dd0123 Seg 19 Nov 2018, 21:52

Em um círculo de raio R inscreve-se... 390f980e0ecdc9b4272db2902d6cf464

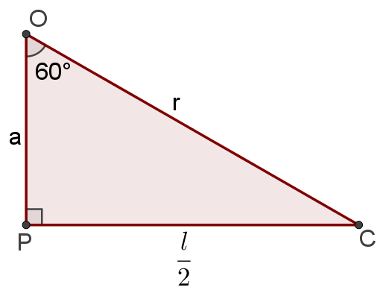
Em um círculo de raio R inscreve-se... Triangulo-poc

Em um círculo de raio R inscreve-se... Circle

\sin 60^{\circ}=\frac{l}{2R}\Leftrightarrow \frac{\sqrt{3}}{2}=\frac{l}{2R}\Leftrightarrow R\sqrt{3}=l \\ \acute{a}rea\: tri\hat{a}ngulo \: equil\acute{a}tero \mapsto \frac{l^{2}\sqrt{3}}{4} \\ \\ \frac{l^{2}\sqrt{3}}{4}=1 \Leftrightarrow \frac{(R\sqrt{3})^{2}\sqrt{3}}{4}=1\Leftrightarrow \frac{3R^{2}\sqrt{3}}{4}=1\Leftrightarrow R^{2}=\frac{4\sqrt{3}}{9}
\\ \acute{a}rea\:hex\acute{a}gono \: regular (A) \mapsto 6.\frac{(4R)^{2}\sqrt{3}}{4} \\ A=6.\frac{16R^{2}\sqrt{3}}{4}\Leftrightarrow A=6.4.(\frac{4\sqrt{3}}{9}).\sqrt{3}\Leftrightarrow A=32\: cm^{2}

por dd0123 Seg 19 Nov 2018, 21:54

Desculpe Elcio, mandei mesmo com a sua resposta só pra não perder o trabalho Laughing

por **Elcioschin** Seg 19 Nov 2018, 22:23

Sua solução melhorou a compreensão, com as figuras

por Lele9898 Seg 19 Nov 2018, 22:25

Muitíssimo obrigada, Elcio e ddmr0123!! Vocês me ajudaram bastante!

por **Medeiros** Ter 20 Nov 2018, 02:08

Lele

O Élcio e o ddmr apresentaram uma solução ortodoxa. Aproveitando a figura do ddmr vou apresentar uma heterodoxa -- porque adoro soluções heterodoxas desde que faça menos contas.

Inscritos no mesmo círculo, é visível que o triângulo equilátero tem metade da área do hexágono regular -----> Sh = 2.St
Então, se num círculo de raio R o triângulo tem área St=1 cm², o hexágono terá Sh=2 cm².
Atente que o lado do hexágono é igual ao raio: L = R.

Inscrito num círculo de raio R' o hexágono regular terá lado L'=R' , area S'h e será semelhante ao anterior. Pela propriedade de figuras semelhantes, "a razão entre as áreas é igual ao quadrado da razão entre lados homólogos".
S'h/Sh = (L'/L)²
como L=R e L'=4.R
S'h/2 = (4R/R)² -----> S'h/2 = 4² -----> S'h = 32 cm²