Área do Triângulo Inscrito na Circunferência
2 participantes
Página 1 de 1
 Área do Triângulo Inscrito na Circunferência
Área do Triângulo Inscrito na Circunferência
Os vértices de um triângulo inscrito em uma circunferência dividem esta em três arcos de comprimentos 3, 4 e 5. A área do triângulo é igual a:
a) 6
b)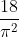
c)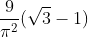
d)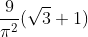
e)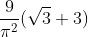
a) 6
b)
c)
d)
e)
Última edição por luccarhaddad em Qua 07 Nov 2018, 10:56, editado 1 vez(es)
luccarhaddad- Iniciante
- Mensagens : 19
Data de inscrição : 12/07/2017
Idade : 23
Localização : São João Del Rei, Minas Gerais, Brasil
 Re: Área do Triângulo Inscrito na Circunferência
Re: Área do Triângulo Inscrito na Circunferência
Bem, você começa fazendo uma regra de três para calcular os ângulos do triângulo.
360 --- 12 (circunferência, soma dos arcos )
2x --- 5 ( sendo x o ângulo que olha para o arco valendo 5)
2x = 150 x = 75
E assim você faz para os outros ângulos.
PS: na regra de três você multiplica o angulo, no caso x por 2 porque é inscrito.
Após isso você vai traçar do centro do círculo até os vértices ( Raios do círculo )
Feito isso você sabe os ângulos formados pelos raios, os ângulos centrais ( 2 vezes o ângulo que olha para o mesmo arco que ele Ex.: 2x )
Agora você faz as áreas dos triângulos formados pelos raios dentro do triângulo maior ( 3 triângulos )
Sendo a área a seguinte: lado.lado.(seno do ângulo formado pelo encontro de tais lados ) Utilize o ângulo central !
Soma as áreas encontradas em função de R
Depois você sabe que 2∏R = 12 ⇒ R = 6/∏
Sabendo R em função de ∏ você sabe a área do triângulo em função de ∏
Resposta: E.
Se não entendeu algo diz ai que explico, Abraços.




EDIT¹.: CONSIDERE ∏ COMO PI
360 --- 12 (circunferência, soma dos arcos )
2x --- 5 ( sendo x o ângulo que olha para o arco valendo 5)
2x = 150 x = 75
E assim você faz para os outros ângulos.
PS: na regra de três você multiplica o angulo, no caso x por 2 porque é inscrito.
Após isso você vai traçar do centro do círculo até os vértices ( Raios do círculo )
Feito isso você sabe os ângulos formados pelos raios, os ângulos centrais ( 2 vezes o ângulo que olha para o mesmo arco que ele Ex.: 2x )
Agora você faz as áreas dos triângulos formados pelos raios dentro do triângulo maior ( 3 triângulos )
Sendo a área a seguinte: lado.lado.(seno do ângulo formado pelo encontro de tais lados ) Utilize o ângulo central !
Soma as áreas encontradas em função de R
Depois você sabe que 2∏R = 12 ⇒ R = 6/∏
Sabendo R em função de ∏ você sabe a área do triângulo em função de ∏
Resposta: E.
Se não entendeu algo diz ai que explico, Abraços.
EDIT¹.: CONSIDERE ∏ COMO PI
Hugo Leandro Antunes- Iniciante
- Mensagens : 4
Data de inscrição : 06/11/2018
Idade : 20
Localização : Rio de Janeiro
 Re: Área do Triângulo Inscrito na Circunferência
Re: Área do Triângulo Inscrito na Circunferência
Valeu Hugo, deu certo aqui!Hugo Leandro Antunes escreveu:Bem, você começa fazendo uma regra de três para calcular os ângulos do triângulo.
360 --- 12 (circunferência, soma dos arcos )
2x --- 5 ( sendo x o ângulo que olha para o arco valendo 5)
2x = 150 x = 75
E assim você faz para os outros ângulos.
PS: na regra de três você multiplica o angulo, no caso x por 2 porque é inscrito.
Após isso você vai traçar do centro do círculo até os vértices ( Raios do círculo )
Feito isso você sabe os ângulos formados pelos raios, os ângulos centrais ( 2 vezes o ângulo que olha para o mesmo arco que ele Ex.: 2x )
Agora você faz as áreas dos triângulos formados pelos raios dentro do triângulo maior ( 3 triângulos )
Sendo a área a seguinte: lado.lado.(seno do ângulo formado pelo encontro de tais lados ) Utilize o ângulo central !
Soma as áreas encontradas em função de R
Depois você sabe que 2∏R = 12 ⇒ R = 6/∏
Sabendo R em função de ∏ você sabe a área do triângulo em função de ∏
Resposta: E.
Se não entendeu algo diz ai que explico, Abraços.


EDIT¹.: CONSIDERE ∏ COMO PI
luccarhaddad- Iniciante
- Mensagens : 19
Data de inscrição : 12/07/2017
Idade : 23
Localização : São João Del Rei, Minas Gerais, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Área do triângulo inscrito no paralelogramo
» Area do retangulo inscrito no triangulo
» Area do circulo inscrito no triangulo
» Área de um triângulo equilátero inscrito
» Area do circulo inscrito no triangulo
» Area do retangulo inscrito no triangulo
» Area do circulo inscrito no triangulo
» Área de um triângulo equilátero inscrito
» Area do circulo inscrito no triangulo
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












