Permutação com Repetição

por popcorn12345 Qua 24 Out 2018, 10:40

Com relação aos anagramas que podem ser formados com as letras da palavra “OLIMPÍADAS”, assinale (V) para as verdadeiras e (F) para as falsas.

a) O total de anagramas que podem ser formados é 3 628 800.

b) Podemos formar 604 800 anagramas que iniciam por consoante e terminam em vogal.

c) A quantidade de anagramas que não possuem 2 vogais juntas é 21 600.

d) Existem 30 240 anagramas que possuem as letras O, L, I juntas.

por **Mateus Meireles** Qua 24 Out 2018, 11:20

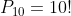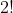Se as letras fossem diferentes, obteríamos $Permutação com Repetição Gif$ anagramas. Como os $Permutação com Repetição Gif$ são iguais, contamos cada anagrama $Permutação com Repetição Gif$ vezes. Analogamente, contamos 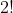$Permutação com Repetição Gif$ cada anagrama por serem iguais os 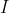$Permutação com Repetição Gif$ . Logo,

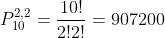
$Permutação com Repetição Gif$

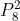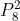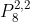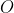
b) Há 5 opções para a primeira letra (L, M, P, D, S) e $Permutação com Repetição Gif$ terminadas em $Permutação com Repetição Gif$ . Da mesma forma, 5 opções para a primeira letra (L, M, P, D, S) e $Permutação com Repetição Gif$ terminadas em $Permutação com Repetição Gif$ , e, por fim, 5 opções para a primeira letra (L, M, P, D, S) e $Permutação com Repetição Gif$ terminadas em $Permutação com Repetição Gif$

A resposta é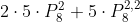 $Permutação com Repetição Gif$

c) Existem muitas ideias para esse item.. Deixarei uma

O número de formas de arrumarmos as letras que não são vogais é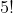 $Permutação com Repetição Gif$ . Por exemplo, uma dessas configurações é

⠀

_ L _ M _ P _ D _ S _

1 2 3 4 5 6

Agora temos que colocar as vogais nos locais assinalados. Como em nenhum espaço pode ficar mais de uma vogal, ocuparemos 5 espaços (1 para cada vogal) e deixaremos 1 espaço vazio. O número de maneiras de escolher os espaços ocupados é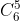 $Permutação com Repetição Gif$ . Escolhido esses espaços, é possível, ainda, permutar as vogais entre si, 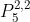$Permutação com Repetição Gif$ (elementos repetidos).

A resposta é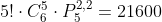 $Permutação com Repetição Gif$

Depois eu escrevo os outros itens.

por **Mateus Meireles** Sex 26 Out 2018, 23:47

popcorn12345 escreveu:d) Existem 30 240 anagramas que possuem as letras O, L, I juntas.

Tudo se passa como se OLI fosse uma única letra. Primeiramente, devemos escolher a ordem em que as letras O, L, I aparecerão. Há 3! modos. Depois, devemos arrumar me fila 8 objetos: o bloco das letras O,L,I e as 7 letras M,P,Í,A,D,A,S. Há modos de fazermos isso.

A resposta é 3! x 8!/2! = 120960

por popcorn12345 Dom 28 Out 2018, 12:20

Letra C)
Não entendi o motivo pelo qual ficou seis espaços vazios.

_ L _ M _ P _ D _ S _

1 2 3 4 5 6

Se:
vogais da palavra: O, I, I, A, A "cinco".
consoantes da palavra: [size=15]L, M, P, D, S "cinco".[/size]

Letra b)
A resposta não seria

C, __, __, __, __, __, __, __, __, V

5C, __, __, __, __, __, __, __, __, A      =   2. P₈²

5C, __, __, __, __, __, __, __, __, I       =   2. P₈²

5, __, __, __, __, __, __, __, __, 0      =   P₈^2,2

Resposta = 5*4. P₈²+ 5* P₈^2,2 ?

Fico no aguardo

por **Mateus Meireles** Dom 28 Out 2018, 18:13

popcorn12345 escreveu:Letra C)
Não entendi o motivo pelo qual ficou seis espaços vazios.

Há um espaço disponível antes da letra L, um espaço disponível entre a letra L e a letra M, um espaço disponível entre a letra M e a letra P, etc. Os espaços disponíveis estão representados por " _ "

Obviamente esse comentário considera o anagrama mostrado no meu primeiro comentário. A ideia é que haverá um espaço antes da primeira consoante, um espaço disponível entre a primeira e a segunda,.. etc.

popcorn12345 escreveu:A resposta não seria

C, __, __, __, __, __, __, __, __, V

5C, __, __, __, __, __, __, __, __, A      =   2. P₈²

5C, __, __, __, __, __, __, __, __, I       =   2. P₈²

5, __, __, __, __, __, __, __, __, 0      =   P₈^2,2

Resposta = 5*4. P₈²+ 5* P₈^2,2 ?

Fico no aguardo

Irei responder o seu questionamento com outro problema.

Quantos anagramas da palavra CASA começam por consoante e terminam por vogal?

Segundo o seu raciocínio, 2 x 2 x 2 = 8

Veja, porém, que os A são indiferentes, isto é, não devemos considerar duas possibilidades para a última casa, mas apenas uma

Observe:

CASA
CSAA
SACA
SCAA

Ou seja, a forma correta de contarmos é: 2 opções para a primeira letra, 1 para a última (deve terminar em A) e a permutação de duas letras entre as 2 últimas, 2

Daí, a resposta é 2 x 2 = 4, o que confere com o que foi analisado anteriormente.

A contagem para o seu problema está correta, tente visualizar agora.