Algebra Linear - Prova
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Algebra Linear - Prova
por heliom Qua 17 Out 2018, 21:42
Seja A =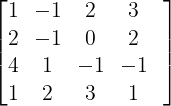 
a) Calcule a inversa de A; isto é,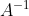
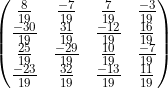
b) Se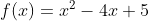
, determine f(A).
Qual seria a ajuda? — O que fazer no item b? Seria substituir cada elemento da matriz inversa, e substituir na função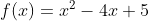 e achar uma nova matriz f(a)?
Agradeço a algum amigo do fórum em ajudar a interpretar o iitem b.
Grato
a) Calcule a inversa de A; isto é,
b) Se
Qual seria a ajuda? — O que fazer no item b? Seria substituir cada elemento da matriz inversa, e substituir na função
Agradeço a algum amigo do fórum em ajudar a interpretar o iitem b.
Grato
heliom- Iniciante
- Mensagens : 45
Data de inscrição : 18/05/2013
Idade : 57
Localização : Rio de Janeiro
Re: Algebra Linear - Prova
por Elcioschin Qua 17 Out 2018, 22:39
f(A) = A² - 4.A + 5
Calcule A² e 4.A e depois calcule f(A)
Calcule A² e 4.A e depois calcule f(A)
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Algebra Linear - Prova
por heliom Qui 18 Out 2018, 18:06
Prof. Elcioschin,
Grato pelo retorno.
*** Por favor me corrija se eu estiver errado ***
1) Elevo ao quadro a matriz A; A²
2) multiplico a matriz A, pelo escalar 4 - ou seja - multiplico toda a matriz A por 4; (4A)
3) depois faço a soma de 5 em toda matriz A;
Daí faço a operação A² - 4A + 5, onde terei f(A)
É isso?
Grato pelo retorno.
*** Por favor me corrija se eu estiver errado ***
1) Elevo ao quadro a matriz A; A²
2) multiplico a matriz A, pelo escalar 4 - ou seja - multiplico toda a matriz A por 4; (4A)
3) depois faço a soma de 5 em toda matriz A;
Daí faço a operação A² - 4A + 5, onde terei f(A)
É isso?
heliom- Iniciante
- Mensagens : 45
Data de inscrição : 18/05/2013
Idade : 57
Localização : Rio de Janeiro
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
heliom- Iniciante
- Mensagens : 45
Data de inscrição : 18/05/2013
Idade : 57
Localização : Rio de Janeiro
Tópicos semelhantes» Seja T é uma aplicação linear de um espaço vetorial (Algebra Linear)
» 5.Ache uma aplicação linear T : R^4 --> R^3 (Algebra linear)
» algebra linear:Ache uma aplicação linear
» Algebra Linear - Dependência Linear
» ALGEBRA LINEAR - DEPENDENCIA LINEAR
» 5.Ache uma aplicação linear T : R^4 --> R^3 (Algebra linear)
» algebra linear:Ache uma aplicação linear
» Algebra Linear - Dependência Linear
» ALGEBRA LINEAR - DEPENDENCIA LINEAR
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
