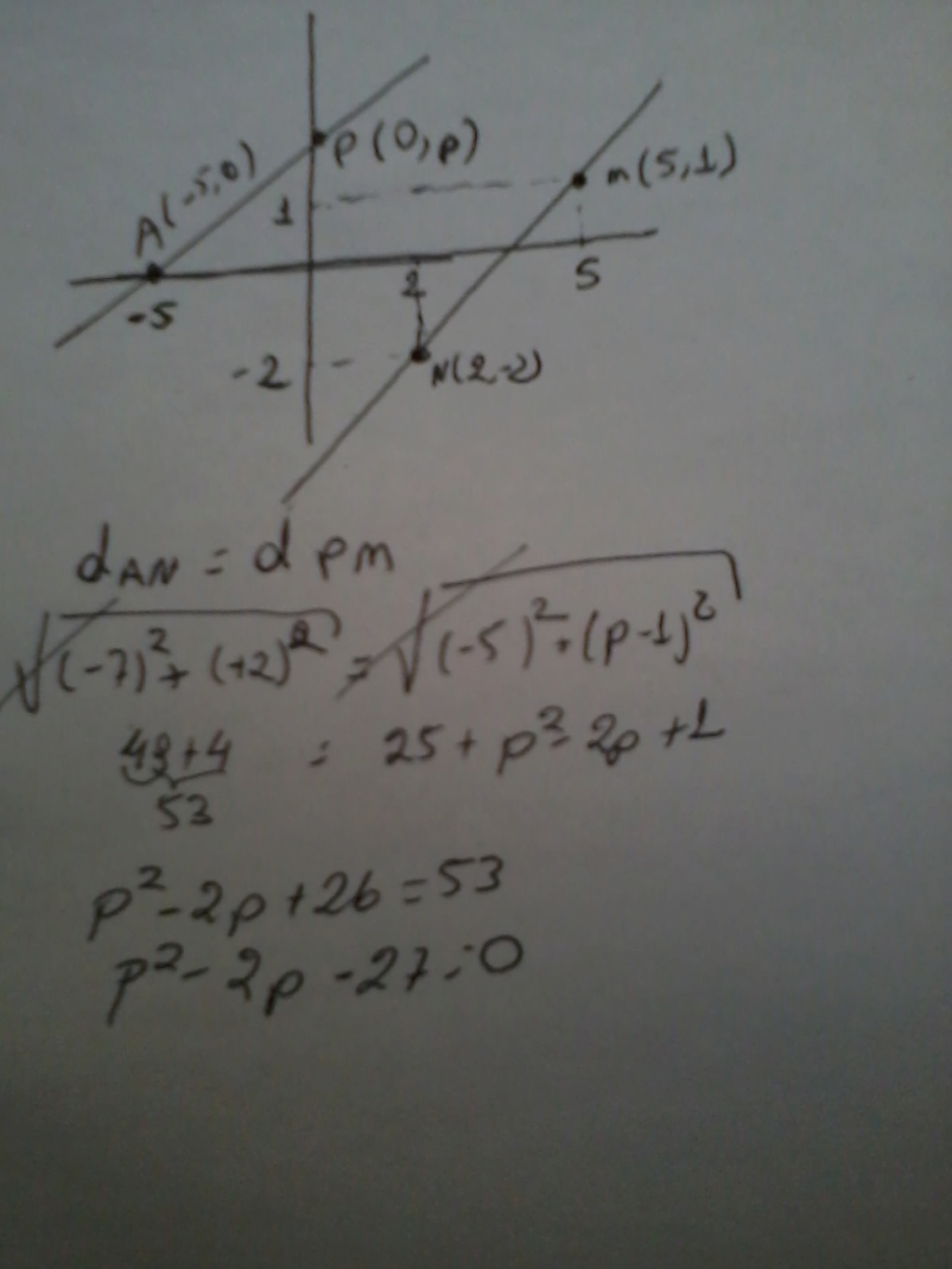Em um sistema de eixos cartesianos ortogonais, a reta s
2 participantes
Página 1 de 1
 Em um sistema de eixos cartesianos ortogonais, a reta s
Em um sistema de eixos cartesianos ortogonais, a reta s
Em um sistema de eixos cartesianos ortogonais, a reta s contém o ponto (– 5, 0) e é paralela à reta MN, sendo M = (5, 1) e N = (2, – 2). Sabendo-se que a reta s intersecta o eixo das ordenadas no ponto P, é correto afirmar que a equação da reta s e a ordenada do ponto P são, respectivamente,
(A) – x + 3y – 5 = 0 e y = –5
(B) – x – y + 5 = 0 e y = 5
(C) x – 3y + 5 = 0 e y = –5
(D) x – y + 5 = 0 e y = 5
(E) – x – y – 5 = 0 e y = 5
Resposta = d
(A) – x + 3y – 5 = 0 e y = –5
(B) – x – y + 5 = 0 e y = 5
(C) x – 3y + 5 = 0 e y = –5
(D) x – y + 5 = 0 e y = 5
(E) – x – y – 5 = 0 e y = 5
Resposta = d

powermetal- Jedi

- Mensagens : 327
Data de inscrição : 12/09/2012
Idade : 32
Localização : minas

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Re: Em um sistema de eixos cartesianos ortogonais, a reta s
Re: Em um sistema de eixos cartesianos ortogonais, a reta s

powermetal- Jedi

- Mensagens : 327
Data de inscrição : 12/09/2012
Idade : 32
Localização : minas
 Re: Em um sistema de eixos cartesianos ortogonais, a reta s
Re: Em um sistema de eixos cartesianos ortogonais, a reta s
Sua solução dá errado porque parte de uma mentira. Aquelas distâncias tem chance de serem iguais somente se os segmentos AP e MN tiverem mesma medida. MN = 3√3, vc deveria obrigar AP a ter essa medida; mas com os interceptos de s isto claramente não ocorre.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Tópicos semelhantes
Tópicos semelhantes» Em um mesmo sistema de eixos cartesianos ortogonais, as
» Em um sistema de eixos cartesianos ortogonais, foi dese
» Num sistema de eixos
» Circunferêcia tangencia eixos e reta
» Sistema cartesiano, equação da reta e da circunferencia
» Em um sistema de eixos cartesianos ortogonais, foi dese
» Num sistema de eixos
» Circunferêcia tangencia eixos e reta
» Sistema cartesiano, equação da reta e da circunferencia
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos