Geometria espacial - cones

Uma ampulheta é formada por dois cones idênticos. Inicialmente, o cone superior está cheio de areia e o cone inferior está vazio. A areia flui do cone superior para o inferior com vazão constante. O cone superior se esvazia em exatamente quatro horas e meia. Quanto tempo demora até que a altura da areia no cone inferior seja metade da altura da areia do cone superior?

a) 4 h
b) 3 h e 30 min
c) 3 h e 10 min
d) 3 h
e) 1 h e 30 min

Gabarito - letra C

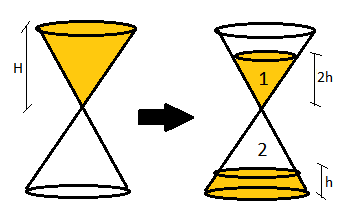
 Vamos chamar o volume total do cone de V_c e o volume de areia do cone inferior de V_i. Note que V_c = V₁ + V_i (figura da esquerda) e V_c = V₂ + V_i (figura da direita). Logo, concluímos que V₁ = V₂, e consequentemente, que h₂ = h₁ = 2h. Além disso, como H = h₂ + h, concluímos que H = 3h. 

Agora o problema pode ser encarado da seguinte forma: inicialmente tínhamos o cone superior cheio, com areia na altura H = 3h. Posteriormente, vaza areia até a altura atingir 2h. Vamos descobrir o volume de areia que vazou :



Além disso, como a velocidade de vazão é constante, podemos fazer uma regra de 3 entre as variações de volume e de tempo. Como o volume total V_c vaza em 4,5 h: