Área hachurada

por JEABM Qua 25 Jul 2018, 21:44

calcular a área da superfície sombreada em função de r.
Gab: pi . r^2

por Matemathiago Qua 25 Jul 2018, 22:38

por JEABM Qua 25 Jul 2018, 22:52

N entendi como achou a área S2...poderia explicar melhor grato

por **Elcioschin** Qua 25 Jul 2018, 22:53

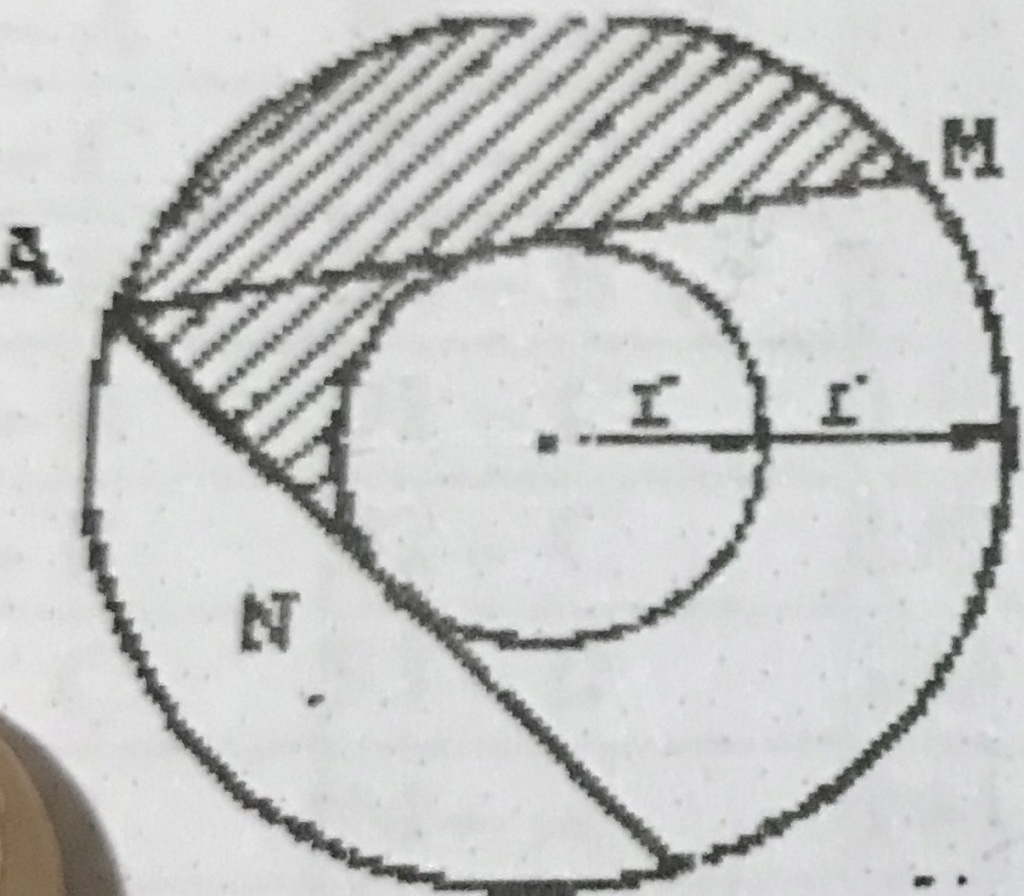
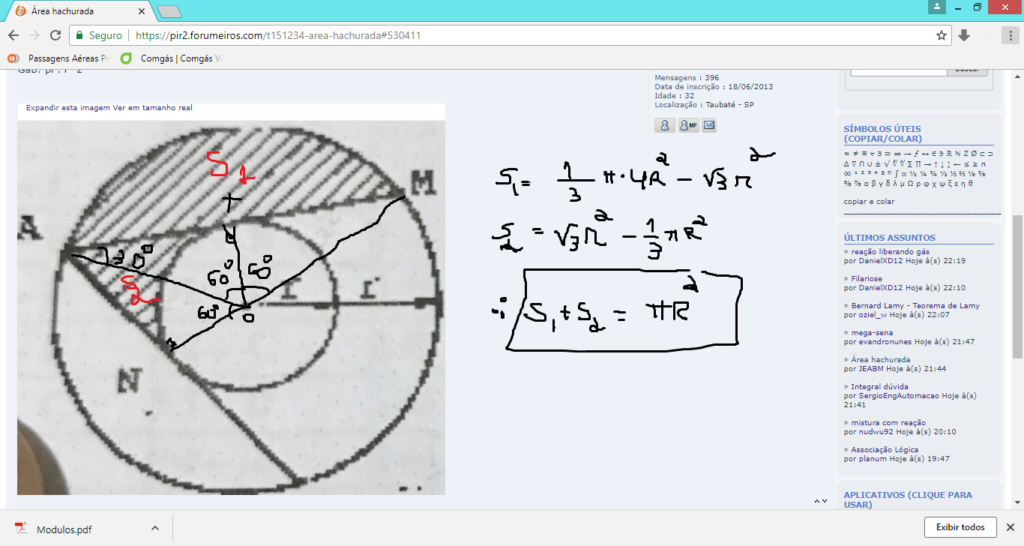
Seja O o centro dos dois círculos e B, C os dois pontos de tangência. Trace OA e OM

OA = OM = 2.r ---> OB = OC = r ---> cosAÔB = OB/OA = r/2.r = 1/2 ---> AÔB = 60º ---> AÔM = 120º

AB = OA.sen60º ---> AB = 2.r.(√3/2) ---> AB = r.√3

Área do segmento circular superior = área do setor de 120º e raio 2.r - 2*área triângulo AOB --->

S1 = pi.(2.r)²/3 - 2.(AB.OB/2) ---> S1 = 4.pi.r²/3 - 2.(r.√3).r ---> S1 = pi.r²/3 - r².√3

Área do "triângulo curvilíneo" hachurado = 2.Área triângulo AOB - área setor 120º e raio r

S2 = r².√3 - pi.r²/3

S = S1 + S2 ---> S = (pi.r²/3 - r².√3) + (r².√3 - pi.r²/3) ---> S = pi.r²